题目内容
A,B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1和X2的分布列分别为| X1 | 5% | 10% | X2 | 2% | 8% | 12% | |
| P | 0.8 | 0.2 | P | 0.2 | 0.5 | 0.3 |
(Ⅱ)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.(注:D(aX+b)=a2DX)
分析:(1)Y1和Y2分别表示投资项目A和B所获得的利润,根据两个投资项目的利润率分别为随机变量X1和X2的分布列,可以得到Y1和Y2的分布列,得到分布列,余下的问题只是运算问题,分别求出变量的方差.
(2)由题意知f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和,写出用x表示的方差的解析式,结合二次函数的最值问题,得到结果.
(2)由题意知f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和,写出用x表示的方差的解析式,结合二次函数的最值问题,得到结果.
解答:解:(Ⅰ)∵Y1和Y2分别表示投资项目A和B所获得的利润,
根据两个投资项目的利润率分别为随机变量X1和X2的分布列
可以得到Y1和Y2的分布列分别为
EY1=5×0.8+10×0.2=6,
DY1=(5-6)2×0.8+(10-6)2×0.2=4,
EY2=2×0.2+8×0.5+12×0.3=8,
DY2=(2-8)2×0.2+(8-8)2×0.5+(12-8)2×0.3=12.
(Ⅱ)f(x)=D(
Y1)+D(
Y2)
=(
)2DY1+(
)2DY2
=
[x2+3(100-x)2]
=
(4x2-600x+3×1002),
当x=
=75时,
f(x)=3为最小值.
根据两个投资项目的利润率分别为随机变量X1和X2的分布列
可以得到Y1和Y2的分布列分别为
| Y1 | 5 | 10 | Y2 | 2 | 8 | 12 | |
| P | 0.8 | 0.2 | P | 0.2 | 0.5 | 0.3 |
DY1=(5-6)2×0.8+(10-6)2×0.2=4,
EY2=2×0.2+8×0.5+12×0.3=8,
DY2=(2-8)2×0.2+(8-8)2×0.5+(12-8)2×0.3=12.
(Ⅱ)f(x)=D(
| x |
| 100 |
| 100-x |
| 100 |
=(
| x |
| 100 |
| 100-x |
| 100 |
=
| 4 |
| 1002 |
=
| 4 |
| 1002 |
当x=
| 600 |
| 2×4 |
f(x)=3为最小值.
点评:本题考查离散型随机变量的分布列和期望,这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
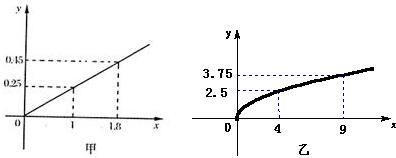

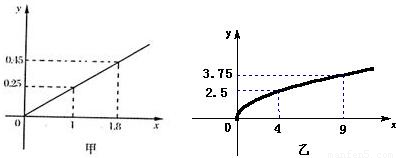

 、
、 ,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)
,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)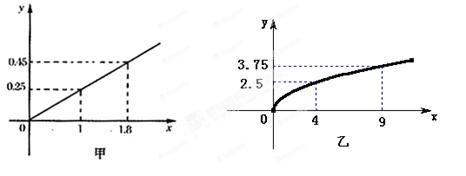
 万元投资A项目, 10-x万元投资B项目.h(x)表示投资A项目所得利润与投资B项目所得利润之和.求h(x)的最大值,并指出x为何值时,h(x)取得最大值.
万元投资A项目, 10-x万元投资B项目.h(x)表示投资A项目所得利润与投资B项目所得利润之和.求h(x)的最大值,并指出x为何值时,h(x)取得最大值.