Question

（本小题满分12分）设直线l（斜率存在）交抛物线y²＝2px（p＞0，且p是常数）于两个不同点A（x₁，y₁），B（x₂，y₂），O为坐标原点，且满足＝x₁x₂＋2（y₁＋y₂）．

   （1）求证：直线l过定点；

   （2）设（1）中的定点为P，若点M在射线PA上，满足，求点M

的轨迹方程．

 

Answer 1

【答案】

（1）直线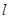过定点（0，2）

（2）点M的轨迹方程为

【解析】解：（I）设直线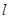的方程为

由                  …………2分

由题知

且                                       …………3分

又

                                                      …………4分

∴直线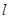的斜率k与p之间的关系为              …………4分

由（I）有                              …………5分

又

                                                      …………7分

则

∴直线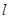的方程为

∴直线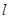过定点（0，2）                                 …………8分

   （II）分别过A、M、B向y轴作垂线，垂足分别为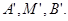

设，可得

…………10分

即…①          …………12分

将①代入

又                        …②

由①②消去k，得

∴点M的轨迹方程为        …………14分