题目内容
如图,在边长为1的正方形OABC内取一点P(x,y),求:
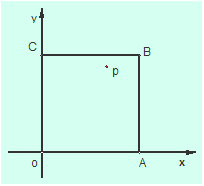
(1)点P到原点距离小于1的概率;
(2)以x,y,1为边长能构成三角形的概率;
(3)以x,y,1为边长能构成锐角三角形的概率

(1)点P到原点距离小于1的概率;
(2)以x,y,1为边长能构成三角形的概率;
(3)以x,y,1为边长能构成锐角三角形的概率
(1)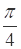 (2)
(2)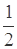 (3)1-
(3)1-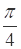
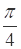 (2)
(2)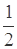 (3)1-
(3)1-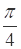
试题分析:解:满足条件的正方形ABCD,如下图示:
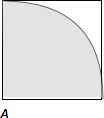
其中满足动点P到定点A的距离|PA|<1的平面区域如图中阴影所示:则正方形的面积S正方形=1,阴影部分的面积S阴影=
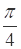 故动点P到定点A的距离|PA|<1的概率P=
故动点P到定点A的距离|PA|<1的概率P=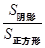 =
=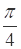
(2)结合三边的不等关系,结合线性规划来得到概率值为
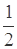
(3)以x,y,1为边长能构成锐角三角形的概率,那么根据余弦定理三边的平方关系来求解,得到结论为1-
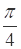
故答案为:
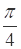 ,
,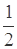 ,1-
,1-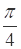
点评:解决的关键是理解阴影部分的面积的表示和整个基本事件空间的区域面积来求解,属于基础题。

练习册系列答案
相关题目
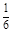 .甲、乙、丙三位同学每人购买了一瓶该饮料.
.甲、乙、丙三位同学每人购买了一瓶该饮料. ,求随机变量
,求随机变量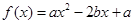 (
(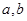
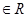 )
)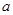 从集合
从集合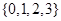 中任取一个元素,
中任取一个元素, 从集合
从集合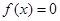 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;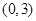 中任取一个数,
中任取一个数, 中任取一个数
中任取一个数