题目内容
已知向量 ,且
,且 与
与 的夹角为锐角,则实数λ的取值范围是 .
的夹角为锐角,则实数λ的取值范围是 .
【答案】分析:由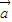 与
与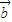 的夹角为锐角,则
的夹角为锐角,则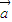 •
•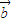 >0,根据向量
>0,根据向量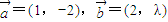 ,我们要以构造一个关于λ的不等式,解不等式即可得到λ的取值范围,但要特别注意
,我们要以构造一个关于λ的不等式,解不等式即可得到λ的取值范围,但要特别注意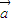 •
•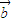 >0还包括
>0还包括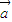 与
与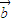 同向(
同向(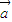 与
与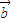 的夹角为0)的情况,讨论后要去掉使
的夹角为0)的情况,讨论后要去掉使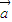 与
与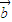 同向(
同向(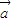 与
与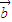 的夹角为0)的λ的取值.
的夹角为0)的λ的取值.
解答:解:∵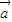 与
与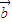 的夹角为锐角
的夹角为锐角
∴ •
•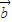 >0
>0
即2-2λ>0
解得λ<1
当λ=-4时,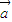 与
与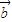 同向
同向
∴实数λ的取值范围是(-∞,-4)∪(-4,1)
故答案为:(-∞,-4)∪(-4,1)
点评:本题考查的知识点是向量数量积的性质及运算律,由两个向量夹角为锐角,两个向量数量积大于0,我们可以寻求解答的思路,但本题才忽略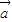 •
•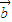 >0还包括
>0还包括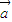 与
与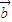 同向(
同向(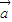 与
与 的夹角为0)的情况,导致实数λ的取值范围扩大.
的夹角为0)的情况,导致实数λ的取值范围扩大.
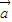 与
与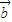 的夹角为锐角,则
的夹角为锐角,则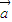 •
•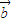 >0,根据向量
>0,根据向量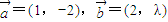 ,我们要以构造一个关于λ的不等式,解不等式即可得到λ的取值范围,但要特别注意
,我们要以构造一个关于λ的不等式,解不等式即可得到λ的取值范围,但要特别注意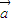 •
•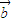 >0还包括
>0还包括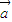 与
与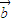 同向(
同向(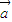 与
与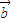 的夹角为0)的情况,讨论后要去掉使
的夹角为0)的情况,讨论后要去掉使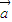 与
与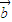 同向(
同向(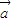 与
与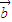 的夹角为0)的λ的取值.
的夹角为0)的λ的取值.解答:解:∵
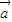 与
与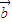 的夹角为锐角
的夹角为锐角∴
 •
•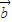 >0
>0即2-2λ>0
解得λ<1
当λ=-4时,
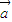 与
与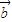 同向
同向∴实数λ的取值范围是(-∞,-4)∪(-4,1)
故答案为:(-∞,-4)∪(-4,1)
点评:本题考查的知识点是向量数量积的性质及运算律,由两个向量夹角为锐角,两个向量数量积大于0,我们可以寻求解答的思路,但本题才忽略
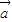 •
•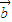 >0还包括
>0还包括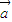 与
与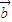 同向(
同向(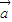 与
与 的夹角为0)的情况,导致实数λ的取值范围扩大.
的夹角为0)的情况,导致实数λ的取值范围扩大. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
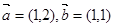 ,且
,且 与
与 的夹角为锐角,则实数
的夹角为锐角,则实数 的取值范围是______.
的取值范围是______.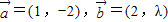 ,且
,且 与
与 的夹角为锐角,则实数λ的取值范围是 .
的夹角为锐角,则实数λ的取值范围是 . ,且
,且 与
与 的夹角为锐角,则实数λ的取值范围是 .
的夹角为锐角,则实数λ的取值范围是 . ,且
,且 与
与 的夹角为锐角,则实数λ的取值范围是 .
的夹角为锐角,则实数λ的取值范围是 .