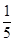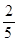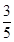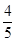题目内容
已知一个矩形由三个相同的小矩形拼凑而成(如图所示),用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,求:

(1)3个矩形都涂同一颜色的概率;
(2)3个小矩形颜色都不同的概率.

(1)3个矩形都涂同一颜色的概率;
(2)3个小矩形颜色都不同的概率.
(1)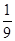 ;(2)
;(2) .
.
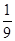 ;(2)
;(2) .
.试题分析:(1)利用分步乘法原理即可得出涂完三个矩形共有
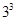 种方法,而3个矩形都涂同一颜色的方法只有三种,利用古典概型的概率计算公式即可得出;(2)“3个小矩形颜色都不同”相当于把三种颜色的全排列数,即
种方法,而3个矩形都涂同一颜色的方法只有三种,利用古典概型的概率计算公式即可得出;(2)“3个小矩形颜色都不同”相当于把三种颜色的全排列数,即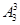 种涂法.利用古典概型的概率计算公式即可得出.
种涂法.利用古典概型的概率计算公式即可得出.试题解析:(1)由题意可知:用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,可以分三步去完成:
涂第一个矩形可有三种方法,涂第二个矩形可有三种方法,涂第三个矩形可有三种方法,
由分步乘法原理可得涂完三个矩形共有
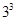 =27种方法,其中3个矩形都涂同一颜色的方法只有三种.
=27种方法,其中3个矩形都涂同一颜色的方法只有三种.设“3个矩形都涂同一颜色”为事件
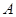 ,则
,则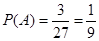 .
.(2)由(1)可知:三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,方法共有
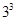 .
.设“3个小矩形颜色都不同”为事件
 ,则事件
,则事件 包括
包括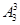 种涂法.
种涂法.由古典概型的概率计算公式可得:
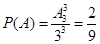 .
.
练习册系列答案
相关题目



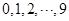 这
这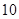 个整数中任意取
个整数中任意取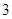 个不同的数作为二次函数
个不同的数作为二次函数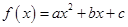 的系数,则使得
的系数,则使得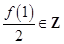 的概率为 .
的概率为 .