题目内容
【题目】函数f（x）=2sin（2x+ 
），g（x）=mcos（2x﹣ 
）﹣2m+3（m＞0），若对任意x1∈[0， 
]，存在x2∈[0， ]，使得g（x1）=f（x2）成立，则实数m的取值范围是（ ）
A.
B.
C.
D.
【答案】D
【解析】解：当x∈[0， 
]时，2x+ 
∈[ ， 
]，sin（2x+ ）∈[ 
，1]， f（x）=2sin（2x+ ）∈[1，2]，
同理可得2x﹣ 
∈[﹣ ， ]，cos（2x﹣ ）∈[ ，1]，
g（x）=mcos（2x﹣ ）﹣2m+3∈[﹣ 
+3，﹣m+3]，
对任意x1∈[0， ]，存在x2∈[0， ]，使得g（x1）=f（x2）成立，
∴ 
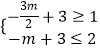，求得1≤m≤ 
，
故选：D．
由题意可得，当x∈[0， ]时，g（x）的值域是f（x）的值域的子集，由此列出不等式组，求得m的范围．
练习册系列答案
相关题目
