题目内容
P是抛物线y 2=4x上一动点，以P为圆心，作与抛物线准线相切的圆，则这个圆一定经过一个定点Q，点Q的坐标是 ．
【答案】
（1，0）
【解析】
试题分析：抛物线y 2=4x的焦点为（1,0），准线方程为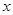
=－1。因为以P为圆心，作与抛物线准线相切的圆，所以P到直准线的距离为半径，由抛物线定义知到焦点距离也为半径，所以所作圆必过焦点，即圆一定经过一个定点Q（1,0）。
考点：本题主要考查抛物线的定义及几何性质。
点评：充分运用抛物线定义，数形结合，使问题巧妙得解。
练习册系列答案
相关题目
F是抛物线y=
x2的焦点，P是该抛物线上的动点，若|PF|=2，则点P的坐标是（ ）
| 1 |
| 4 |
A、（3，
| ||
| B、（±2，1） | ||
| C、（1，4） | ||
| D、（0，0） |
已知点F为抛物线y 2=-8x的焦点，O为原点，点P是抛物线准线上一动点，点A在抛物线上，且|AF|=4，则|PA|+|PO|的最小值为（ ）
| A、6 | ||
B、2+4
| ||
C、2
| ||
D、4+2
|
已知抛物线C1：x2=y，圆C2：x2+（y-4）2=1的圆心为点M
如图，抛物线y=ax2-5ax+4经过△ABC的三个顶点，已知BC∥x轴，点A在x轴上，点C在y轴上，且AC=BC．