题目内容
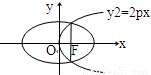
 如图所示,已知抛物线C1:x2=y,圆M:x2+(y-4)2=1,点P是抛物线C1上一点(异于原点),过点P作圆M的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.
如图所示,已知抛物线C1:x2=y,圆M:x2+(y-4)2=1,点P是抛物线C1上一点(异于原点),过点P作圆M的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.分析:设出点P的坐标,利用过点P作圆M的两条切线,交抛物线C1于A,B两点,设出点A,B的坐标,再设出过P的圆M的切线方程,利用交与抛物线C1两点,联立两个方程,利用根与系数之间的关系,得到两切线的斜率的式子,由已知的MP⊥AB,得到方程进而求解.
解答: 解:设点P(x0,x02),A(x1,x12),B(x2,x22),
解:设点P(x0,x02),A(x1,x12),B(x2,x22),
由题意得:x0≠0,x2≠±1,x1≠x2,
设过点P的圆M的切线方程为:y-x02=k(x-x0),
即y=kx-kx0+x02①
则
=1,
即(x02-1)k2+2x0(4-x02)k+(x02-4)2-1=0,
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2应该为上述方程的两个根,
∴k1+k2=
,k1•k2=
;
代入①得:x2-kx+kx0-x02=0,则x1,x2应为此方程的两个根,
故x1=k1-x0,x2=k2-x0
∴kAB=x1+x2=k1+k2-2x0=
-2x0,kMP=
由于MP⊥AB,∴kAB•KMP=-1,
∴[
-2x0]•
=-1
∴x0=±
∴P(±
,
),直线l的方程为:y=±
x+4.
 解:设点P(x0,x02),A(x1,x12),B(x2,x22),
解:设点P(x0,x02),A(x1,x12),B(x2,x22),由题意得:x0≠0,x2≠±1,x1≠x2,
设过点P的圆M的切线方程为:y-x02=k(x-x0),
即y=kx-kx0+x02①
则
| |kx0+4-x02| | ||
|
即(x02-1)k2+2x0(4-x02)k+(x02-4)2-1=0,
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2应该为上述方程的两个根,
∴k1+k2=
| 2x0(x02-4) |
| x02-1 |
| (x02-4)2-1 |
| x02-1 |
代入①得:x2-kx+kx0-x02=0,则x1,x2应为此方程的两个根,
故x1=k1-x0,x2=k2-x0
∴kAB=x1+x2=k1+k2-2x0=
| 2x0(x02-4) |
| x02-1 |
| x02-4 |
| x0 |
由于MP⊥AB,∴kAB•KMP=-1,
∴[
| 2x0(x02-4) |
| x02-1 |
| x02-4 |
| x0 |
∴x0=±
|
∴P(±
|
| 23 |
| 5 |
3
| ||
| 115 |
点评:本题考查直线与圆的位置关系,考查韦达定理的运用,考查斜率的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图所示,已知抛物线y2=2px(p>0)的焦点恰好是椭圆
如图所示,已知抛物线y2=2px(p>0)的焦点恰好是椭圆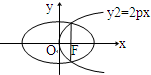
 的右焦点F,且两条曲线的交点连线也过焦点F,则该椭圆的离心率为 .
的右焦点F,且两条曲线的交点连线也过焦点F,则该椭圆的离心率为 .