题目内容
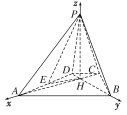
【题目】已知四棱锥P-ABCD的底面为等腰梯形, AB∥CD,AC⊥BD,垂足为H, PH是四棱锥的高,E为AD中点,设![]()
1)证明:PE⊥BC;
2)若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值.

【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)以H为原点,HA,HB,HP所在直线分别为x,y,z轴,建立空间直角
坐标系,利用向量法能证明PE⊥BC;
(2)求出平面PEH的法向量和![]() =(1,0,-1),利用向量法能求出直线PA与平面PEH所成角的正弦值.
=(1,0,-1),利用向量法能求出直线PA与平面PEH所成角的正弦值.
详解:以H为原点,HA,HB,HP所在直线分别为x,y,z轴,建立空间直角坐标系如图,则A(1,0,0),B(0,1,0),
(1)证明:设C(m,0,0),P(0,0,n)(m<0,n>0),则D(0,m,0),E(![]() ,
,![]() ,0).
,0).
可得![]() =(
=(![]() ,
,![]() ,-n),
,-n),![]() =(m,-1,0). 因为
=(m,-1,0). 因为![]() ·
·![]() =
=![]() -
-![]() +0=0,
+0=0,
所以PE⊥BC.
(2)由已知条件可得m=-![]() ,n=1,
,n=1,
故C(-![]() ,0,0),D(0,-
,0,0),D(0,-![]() ,0),E(
,0),E(![]() ,-
,-![]() ,0),
,0),
P(0,0,1).设n=(x,y,z)为平面PEH的法向量,
则![]() 即
即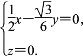
因此可以取n=(1,![]() ,0).
,0).
由![]() =(1,0,-1),可得|cos〈
=(1,0,-1),可得|cos〈![]() ,n〉|=
,n〉|=![]() ,
,
所以直线PA与平面PEH所成角的正弦值为![]() .
.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案【题目】为了解学生暑假阅读名著的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
|
|
|
|
| |
男生 |
|
|
|
|
|
女生 |
|
|
|
|
|
(![]() )从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为
)从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为![]() 的概率?
的概率?
(![]() )若从阅读名著不少于
)若从阅读名著不少于![]() 本的学生中任选
本的学生中任选![]() 人,设选到的男学生人数为
人,设选到的男学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
(![]() )试判断男学生阅读名著本数的方差
)试判断男学生阅读名著本数的方差![]() 与女学生阅读名著本数的方程
与女学生阅读名著本数的方程![]() 的大小.
的大小.
【题目】针对国家提出的延迟退休方案,某机构进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
支持 | 保留 | 不支持 | |
|
|
|
|
|
|
|
|
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“不支持”态度的人中抽取了
个人,已知从持“不支持”态度的人中抽取了![]() 人,求
人,求![]() 的值;
的值;
(2)在接受调查的人中,有![]() 人给这项活动打出的分数如下:
人给这项活动打出的分数如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,把这
,把这![]() 个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过
个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过![]() 的概率.
的概率.
【题目】某商场经营一批进价是每件30元的商品,在市场销售中发现,此商品的销售单价![]() 元与日销售量
元与日销售量![]() 件之间有如下关系
件之间有如下关系![]()
销售单价 | 30 | 40 | 45 | 50 |
日销售量 | 60 | 30 | 15 | 0 |
(1)在平面直角坐标系中,根据表中提供的数据描出实数对![]() 对应的点,并确定
对应的点,并确定![]() 与
与![]() 的一个函数关系式
的一个函数关系式![]() ;
;

(2)设经营此商品的日销售利润为![]() 元,根据上述关系式写出
元,根据上述关系式写出![]() 关于
关于![]() 的函数关系式,
的函数关系式,
并指出销售单价![]() 为多少时,才能获得最大日销售利润。
为多少时,才能获得最大日销售利润。