题目内容
17.设实数集S是满足以下两个条件的集合:①1∉S;②若a∈S,则$\frac{1}{1-a}$∈S.(1)求证:若a∈S,则1-$\frac{1}{a}$∈S;
(2)求证:集合S中至少有三个不同的元素.
分析 (1)根据a∈S,则$\frac{1}{1-a}$∈S,进一步可得$\frac{1}{1-\frac{1}{1-a}}=1-\frac{1}{a}$∈S;
(2)由(1)知,a∈S,$\frac{1}{1-a}$∈S,1-$\frac{1}{a}$∈S,再说明三个数不相等即可.
解答 证明:(1)∵a∈S,a≠0,
∴$\frac{1}{1-a}$∈S,则$\frac{1}{1-\frac{1}{1-a}}=1-\frac{1}{a}$∈S;
(2)由(1)知,a∈S,$\frac{1}{1-a}$∈S,1-$\frac{1}{a}$∈S.
若a=$\frac{1}{1-a}$,则a2-a+1=0,无解,
故a≠$\frac{1}{1-a}$;
同理可证明:a≠1-$\frac{1}{a}$,1-$\frac{1}{a}$≠$\frac{1}{1-a}$.
故集合S中至少有三个不同的元素.
点评 本题考查了元素与集合的关系,是基础题.

练习册系列答案
相关题目
5. 在如图所示的边长为2的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(图中阴影部分)中的概率是( )
在如图所示的边长为2的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(图中阴影部分)中的概率是( )
 在如图所示的边长为2的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(图中阴影部分)中的概率是( )
在如图所示的边长为2的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(图中阴影部分)中的概率是( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
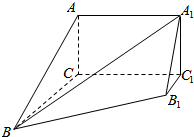 如图,几何体ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面ACC1A1为矩形,平面ACC1A1⊥平面BCC1B1,已知AC=3,BC=AA1=4,BB1=5,B1C1=1
如图,几何体ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面ACC1A1为矩形,平面ACC1A1⊥平面BCC1B1,已知AC=3,BC=AA1=4,BB1=5,B1C1=1