题目内容
已知数列{an}的前五项依次是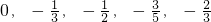 .正数数列{bn}的前n项和为Sn,且
.正数数列{bn}的前n项和为Sn,且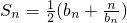 .
.
(I)写出符合条件的数列{an}的一个通项公式;
(II)求Sn的表达式;
(III)在(I)、(II)的条件下,c1=2,当n≥2时,设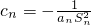 ,Tn是数列{cn}的前n项和,且Tn>logm(1-2m)恒成立,求实数m的取值范围.
,Tn是数列{cn}的前n项和,且Tn>logm(1-2m)恒成立,求实数m的取值范围.
解:(I)由数列的前5项可得,符合条件的数列{an}的一个通项公式为 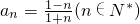 .…(2分)
.…(2分)
(II)因为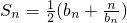 ,即Sn=bn+
,即Sn=bn+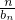 ,2bn>0,所以
,2bn>0,所以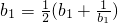 ,解得b1=1,即S1=1.
,解得b1=1,即S1=1.
当n≥2时,bn=Sn-Sn-1,所以,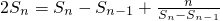 ,∴.
,∴.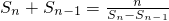 ,即
,即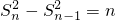 .…(5分)
.…(5分)
所以,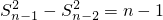 ,
,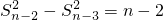 ,…,
,…,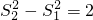 ,
,
累加可得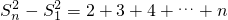 .
.
所以,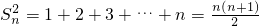 ,即
,即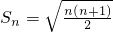 .…..(8分)
.…..(8分)
(III)在(I)、(II)的条件下,c1=2.
当n≥2时,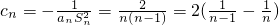 .
.
当n=1时,T1=c1=2;
当n≥2时,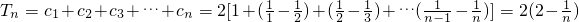 ….(10分)
….(10分)
因为Tn>logm(1-2m)恒成立,即logm(1-2m)恒小于Tn的最小值.
显然,Tn的最小值在n=1时取得,且最小值为2,故有logm(1-2m)<2.…..(12分)
所以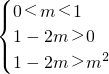 ①,或
①,或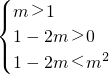 ②.
②.
解①得,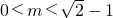 ,不等式组②无解.
,不等式组②无解.
故实数m的取值范围是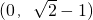 ….(14分)
….(14分)
分析:(I)由数列的前5项的特点,总结归纳可得符合条件的数列{an}的一个通项公式.
(II)由Sn=bn+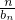 ,求得b1=1,可得S1=1.当n≥2时,由bn=Sn-Sn-1,得
,求得b1=1,可得S1=1.当n≥2时,由bn=Sn-Sn-1,得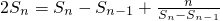 ,化简得
,化简得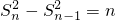 .用累加法求得,
.用累加法求得,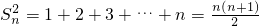 ,从而求得Sn的表达式.
,从而求得Sn的表达式.
(III)先求得Tn的解析式,由Tn>logm(1-2m)恒成立,可得logm(1-2m)恒小于Tn的最小值,根据Tn的最小值在n=1时取得,且最小值为2.故有logm(1-2m)<2.
由此可得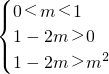 ①,或
①,或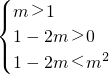 ②.分别求得①和②的解集,再取并集,即得所求.
②.分别求得①和②的解集,再取并集,即得所求.
点评:本题主要考查数列的前n项和与第n项的关系,用累加法进行数列求和,函数的恒成立问题,体现了分类讨论的数学思想,属于难题.
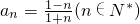 .…(2分)
.…(2分)(II)因为
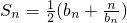 ,即Sn=bn+
,即Sn=bn+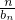 ,2bn>0,所以
,2bn>0,所以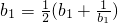 ,解得b1=1,即S1=1.
,解得b1=1,即S1=1.当n≥2时,bn=Sn-Sn-1,所以,
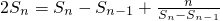 ,∴.
,∴.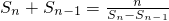 ,即
,即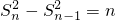 .…(5分)
.…(5分)所以,
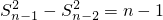 ,
,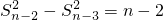 ,…,
,…,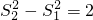 ,
,累加可得
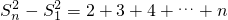 .
.所以,
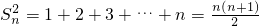 ,即
,即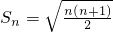 .…..(8分)
.…..(8分)(III)在(I)、(II)的条件下,c1=2.
当n≥2时,
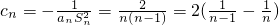 .
.当n=1时,T1=c1=2;
当n≥2时,
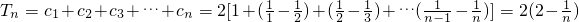 ….(10分)
….(10分)因为Tn>logm(1-2m)恒成立,即logm(1-2m)恒小于Tn的最小值.
显然,Tn的最小值在n=1时取得,且最小值为2,故有logm(1-2m)<2.…..(12分)
所以
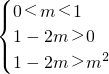 ①,或
①,或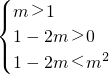 ②.
②.解①得,
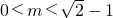 ,不等式组②无解.
,不等式组②无解.故实数m的取值范围是
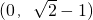 ….(14分)
….(14分)分析:(I)由数列的前5项的特点,总结归纳可得符合条件的数列{an}的一个通项公式.
(II)由Sn=bn+
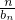 ,求得b1=1,可得S1=1.当n≥2时,由bn=Sn-Sn-1,得
,求得b1=1,可得S1=1.当n≥2时,由bn=Sn-Sn-1,得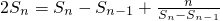 ,化简得
,化简得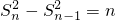 .用累加法求得,
.用累加法求得,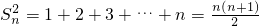 ,从而求得Sn的表达式.
,从而求得Sn的表达式.(III)先求得Tn的解析式,由Tn>logm(1-2m)恒成立,可得logm(1-2m)恒小于Tn的最小值,根据Tn的最小值在n=1时取得,且最小值为2.故有logm(1-2m)<2.
由此可得
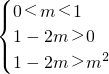 ①,或
①,或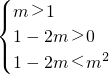 ②.分别求得①和②的解集,再取并集,即得所求.
②.分别求得①和②的解集,再取并集,即得所求.点评:本题主要考查数列的前n项和与第n项的关系,用累加法进行数列求和,函数的恒成立问题,体现了分类讨论的数学思想,属于难题.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |