题目内容
从边长2a的正方形铁片的四个角各截一个边长为x的正方形,然后折成一个无盖的长方体盒子,要求长方体的高度x与底面正方形边长的比不超过正常数t.
(1)把铁盒的容积V表示为x的函数,并指出其定义域;
(2)x为何值时,容积V有最大值.

(1)把铁盒的容积V表示为x的函数,并指出其定义域;
(2)x为何值时,容积V有最大值.

由题意得,V=x(2a-2x)2=4(a-x)2•x
∴
∴0<x≤
∴函数V(x)=4(a-x)2•x的定义域为 (0,
]
V′=4(x-a)•(3x-a)令V′=0得 x=
(1)当
≤
,即 t≥
时,
∵0<x<
时,V′>0.
V(x)为增函数;
<x≤
时,V′<0.V(x)为减函数;
∴V(x)在 (0,
]上有极大值V(
),
∵x=
为唯一驻点,
∴当 x=
时,V有最大值
a3.
(2)当
>
,即 0<t<
时,
∵0<x<
时,V′>0恒成立;
∴V(x)为增函数;
∴当 x=
时,V有最大值
.
∴
|
∴0<x≤
| 2at |
| 1+2t |
∴函数V(x)=4(a-x)2•x的定义域为 (0,
| 2at |
| 1+2t |
V′=4(x-a)•(3x-a)令V′=0得 x=
| a |
| 3 |
(1)当
| a |
| 3 |
| 2at |
| 1+2t |
| 1 |
| 4 |
∵0<x<
| a |
| 3 |
V(x)为增函数;
| a |
| 3 |
| 2at |
| 1+2t |
∴V(x)在 (0,
| 2at |
| 1+2t |
| a |
| 3 |
∵x=
| a |
| 3 |
∴当 x=
| a |
| 3 |
| 16 |
| 27 |
(2)当
| a |
| 3 |
| 2at |
| 1+2t |
| 1 |
| 4 |
∵0<x<
| 2at |
| 1+2t |
∴V(x)为增函数;
∴当 x=
| 2at |
| 1+2t |
| 8a3t |
| (1+2t)3 |

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
 可近似地用函数
可近似地用函数 来刻画.其中:正整数
来刻画.其中:正整数 表示月份且
表示月份且 ,例如
,例如 时表示1月份;
时表示1月份; 和
和 是正整数;
是正整数;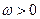 .
.


 ,那么在区间
,那么在区间 中任取一个值
中任取一个值 ,使
,使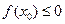 的概率为
的概率为


