题目内容
(2013•湛江二模)对集合A,如果存在x0使得对任意正数a,都存在x∈A,使0<|x-x0|<a,则称x0为集合A的“聚点”,给出下列四个集合:
①{
|n∈Z,n≥0};
②{x∈R|x≠0};
③{
|n∈Z,n≠0};
④Z.
其中以0为“聚点”的集合是( )
①{
| n |
| n+1 |
②{x∈R|x≠0};
③{
| 1 |
| n |
④Z.
其中以0为“聚点”的集合是( )
分析:利用“聚点”的定义可得①的聚点是1,②的聚点是0,③的聚点是0,而④无聚点.
解答:解:①令f(n)=
,则f(n+1)-f(n)=
-
=
>0,即f(n)=
当n∈N时单调递增,则1为其“聚点”,下面给出证明:
取x0=1,对任意正数a,要使0<|
-1|=|
|<a成立,只要取正整数n=[
-1]+2,故1是其“聚点”;
②由实数的稠密性可知:对任意正数a,都存在x=
∈{x∈R|x≠0},使0<|x-0|<a成立,故0是此集合的“聚点”;
③∵
=1-
,由(1)可知:0为集合{
|n∈Z,n≠0},根据“聚点”的定义可知,0是其聚点;
④?n∈Z,且n≠0,则|n|≥1,故取0<a<1,则不存在x∈Z,使0<|x-x0|<a成立,根据“聚点”的定义可知:所给集合不存在聚点.
综上可知:只有②③正确;
故选A.
| n |
| n+1 |
| n+1 |
| n+2 |
| n |
| n+1 |
| 1 |
| (n+1)(n+2) |
| n |
| n+1 |
取x0=1,对任意正数a,要使0<|
| n |
| n+1 |
| 1 |
| n+1 |
| 1 |
| a |
②由实数的稠密性可知:对任意正数a,都存在x=
| a |
| 2 |
③∵
| 1 |
| n+1 |
| n |
| n+1 |
| 1 |
| n |
④?n∈Z,且n≠0,则|n|≥1,故取0<a<1,则不存在x∈Z,使0<|x-x0|<a成立,根据“聚点”的定义可知:所给集合不存在聚点.
综上可知:只有②③正确;
故选A.
点评:正确理解函数的单调性、实数的稠密性、聚点的定义是解题的关键.

练习册系列答案
相关题目
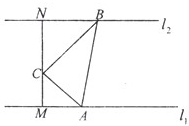 (2013•湛江二模)如图,已知平面上直线l1∥l2,A、B分别是l1、l2上的动点,C是l1,l2之间一定点,C到l1的距离CM=1,C到l2的距离CN=
(2013•湛江二模)如图,已知平面上直线l1∥l2,A、B分别是l1、l2上的动点,C是l1,l2之间一定点,C到l1的距离CM=1,C到l2的距离CN=