题目内容
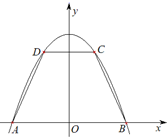 (2012•西城区一模)如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.
(2012•西城区一模)如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.(Ⅰ)求面积S以x为自变量的函数式;
(Ⅱ)若
| |CD| | |AB| |
分析:(Ⅰ)依题意,确定点C的纵坐标、点B的横坐标,从而利用梯形的面积公式,即可求得S关于x的函数式;
(Ⅱ)先确定函数关系式,再求导数,利用分类讨论的数学思想,确定函数的单调性,从而可求S的最大值.
(Ⅱ)先确定函数关系式,再求导数,利用分类讨论的数学思想,确定函数的单调性,从而可求S的最大值.
解答:解:(Ⅰ)依题意,点C的横坐标为x,点C的纵坐标为yC=-x2+9.…(1分)
点B的横坐标xB满足方程-
+9=0,解得xB=3,舍去xB=-3. …(2分)
所以S=
(|CD|+|AB|)•yC=
(2x+2×3)(-x2+9)=(x+3)(-x2+9).…(4分)
由点C在第一象限,得0<x<3.
所以S关于x的函数式为 S=(x+3)(-x2+9),0<x<3.…(5分)
(Ⅱ)由
及0<k<1,得0<x≤3k. …(6分)
记f(x)=(x+3)(-x2+9),0<x≤3k,
则f'(x)=-3x2-6x+9=-3(x-1)(x+3). …(8分)
令f'(x)=0,得x=1. …(9分)
①若1<3k,即
<k<1时,f'(x)与f(x)的变化情况如下:
所以,当x=1时,f(x)取得最大值,且最大值为f(1)=32.…(11分)
②若1≥3k,即0<k≤
时,f'(x)>0恒成立,
所以,f(x)的最大值为f(3k)=27(1+k)(1-k2). …(13分)
综上,
≤k<1时,S的最大值为32;0<k<
时,S的最大值为27(1+k)(1-k2).
点B的横坐标xB满足方程-
| x | 2 B |
所以S=
| 1 |
| 2 |
| 1 |
| 2 |
由点C在第一象限,得0<x<3.
所以S关于x的函数式为 S=(x+3)(-x2+9),0<x<3.…(5分)
(Ⅱ)由
|
记f(x)=(x+3)(-x2+9),0<x≤3k,
则f'(x)=-3x2-6x+9=-3(x-1)(x+3). …(8分)
令f'(x)=0,得x=1. …(9分)
①若1<3k,即
| 1 |
| 3 |
| x | (0,1) | 1 | (1,3k) |
| f'(x) | + | 0 | - |
| f(x) | ↗ | 极大值 | ↘ |
②若1≥3k,即0<k≤
| 1 |
| 3 |
所以,f(x)的最大值为f(3k)=27(1+k)(1-k2). …(13分)
综上,
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查函数模型的构建,考查利用导数知识解决最大值问题,考查分类讨论的数学思想,正确分类是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•西城区一模)如图,AC为⊙O的直径,OB⊥AC,弦BN交AC于点M.若OC=
(2012•西城区一模)如图,AC为⊙O的直径,OB⊥AC,弦BN交AC于点M.若OC=