题目内容
有下列四个命题:
①“若 , 则
, 则 互为相反数”的逆命题;
互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;
④“存在 ,使
,使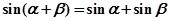 成立”的否定.
成立”的否定.
其中真命题为( )
| A.①② | B.②③ | C.①③ | D.③④ |
C
解析试题分析:解:①“若 , 则
, 则 互为相反数”的逆命题:“若
互为相反数”的逆命题:“若 互为相反数,则
互为相反数,则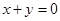 ”是真命题;
”是真命题;
②“全等三角形的面积相等”的否命题:“若两个三角形不全等,则这两个三角形的面积不相等”是假命题;
③“若 ,则
,则 有实根”是真命题,则它的的逆否命题也是真命题;
有实根”是真命题,则它的的逆否命题也是真命题;
④“存在 ,使
,使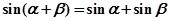 成立”是真命题,它的的否定是假命题.
成立”是真命题,它的的否定是假命题.
故选C.
考点:四种命题及其关系.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
己知命题 “ ”是假命题,则实数
”是假命题,则实数 的取值范围是( )
的取值范围是( )
A. | B.(?1,3) | C. | D.(?3,1) |
“m< ”是“一元二次方程x2+x+m=0有实数解”的 ( )
”是“一元二次方程x2+x+m=0有实数解”的 ( )
| A.充分且必要条件 | B.必要非充分条件 |
| C.充分非必要条件 | D.既不充分也不必要条件 |
命题“ ,使得
,使得 ”的否定是( )
”的否定是( )
A. ,都有 ,都有 | B.不存在 ,使 ,使 |
C. 都有 都有 | D. 使 使 |
若函数 和
和 的定义域、值域都是
的定义域、值域都是 ,则不等式
,则不等式 有解的充要条件是( )
有解的充要条件是( )
A. |
B.有无穷多个 ,使得 ,使得 |
C. |
D. |
命题“若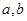 都是奇数,则
都是奇数,则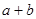 是偶数”的逆否命题是( )
是偶数”的逆否命题是( )
A.若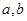 都不是奇数,则 都不是奇数,则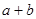 是偶数 是偶数 | B.若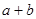 是偶数,则 是偶数,则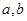 都是奇数 都是奇数 |
C.若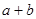 不是偶数,则 不是偶数,则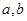 都不是奇数 都不是奇数 | D.若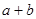 不是偶数,则 不是偶数,则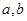 不都是奇数 不都是奇数 |
已知直线l1:k1x+y+1=0与直线l2:k2x+y-1=0,那么“k1=k2”是“l1∥l2”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题p:所有有理数都是实数,命题q:正数的对数都是负数,则下列命题中为真命题的是( )
A.( p)∨q p)∨q | B.p∧q |
C.( p)∧( p)∧( q) q) | D.( p)∨( p)∨( q) q) |
已知空间三条直线a,b,m及平面α,且a,b α.条件甲:m⊥a,m⊥b;条件乙:m⊥α,则“条件乙成立”是“条件甲成立”的( )
α.条件甲:m⊥a,m⊥b;条件乙:m⊥α,则“条件乙成立”是“条件甲成立”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分且必要条件 | D.既非充分也非必要条件 |