题目内容
 已知一几何体的三视图如图,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值.
已知一几何体的三视图如图,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值.
解:由其三视图得:原图形为一直四棱锥,高为6,底面是边长为6的正方形,顶点在点A的正上方.如图①.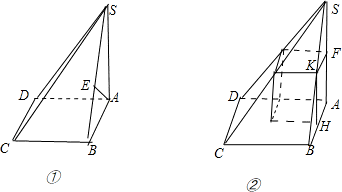
(1)过A做AE⊥SB于E,
因为BC⊥AB,且为直棱锥
所以BC⊥面SAB?BC⊥AE
所以有AE⊥面SCB.
在RT△SAB中,因为两直角边均为6,而且 AE为斜边上的高,所以AE=3 .
.
∴点A到面SBC的距离:3 .
.
(2)如图②,设AF=a,KF=h.
则有 ?KF=SF?6-h=a.
?KF=SF?6-h=a.
所以所求体积:V=S•h=a2•h=a2•(6-a)=6a2-a3.
∴V′=12a-3a2=3a(4-a).
当a>4时,V′<0,
当0<a<4时,V′>0.
∴当a=4时,此时h=2,体积V取最大值,其最大值为:V=6×42-43=32.
所以当棱柱的底面边长为4,高为2时,棱柱的体积最大,最大值为32.
分析:先由其三视图得到原图形为一直四棱锥,高为6,底面是边长为6的正方形,顶点在点A的正上方.
(1)直接过做AE⊥SB于E,根据BC⊥AB以及其为直四棱锥先得到BC⊥AE;再结合AE⊥SB,即可知道求点A到面SBC的距离即为求AE的长,最后在RT△SAB中求出AE的长即可;
(2)先画出大致图象,根据相似比找到高和底面边长之间的惯技,代入体积计算公式,结合导函数知识即可求出当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值.
点评:本题主要考查学生对空间几何体三视图的理解,考查学生的空间想象能力以及运算求解能力.由三视图还原空间几何体的实际形状,一般先从正视图和俯视图考虑,再结合侧视图进行综合分析.

(1)过A做AE⊥SB于E,
因为BC⊥AB,且为直棱锥
所以BC⊥面SAB?BC⊥AE
所以有AE⊥面SCB.
在RT△SAB中,因为两直角边均为6,而且 AE为斜边上的高,所以AE=3
 .
.∴点A到面SBC的距离:3
 .
.(2)如图②,设AF=a,KF=h.
则有
 ?KF=SF?6-h=a.
?KF=SF?6-h=a.所以所求体积:V=S•h=a2•h=a2•(6-a)=6a2-a3.
∴V′=12a-3a2=3a(4-a).
当a>4时,V′<0,
当0<a<4时,V′>0.
∴当a=4时,此时h=2,体积V取最大值,其最大值为:V=6×42-43=32.
所以当棱柱的底面边长为4,高为2时,棱柱的体积最大,最大值为32.
分析:先由其三视图得到原图形为一直四棱锥,高为6,底面是边长为6的正方形,顶点在点A的正上方.
(1)直接过做AE⊥SB于E,根据BC⊥AB以及其为直四棱锥先得到BC⊥AE;再结合AE⊥SB,即可知道求点A到面SBC的距离即为求AE的长,最后在RT△SAB中求出AE的长即可;
(2)先画出大致图象,根据相似比找到高和底面边长之间的惯技,代入体积计算公式,结合导函数知识即可求出当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值.
点评:本题主要考查学生对空间几何体三视图的理解,考查学生的空间想象能力以及运算求解能力.由三视图还原空间几何体的实际形状,一般先从正视图和俯视图考虑,再结合侧视图进行综合分析.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
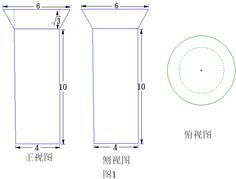 已知一几何体的三视图如图所示,则该几何体的体积为( )
已知一几何体的三视图如图所示,则该几何体的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|

 已知一几何体的三视图如下,其中正视图,侧视图均为矩形,俯视图为等腰直角三角形,则该几何体的体积为
已知一几何体的三视图如下,其中正视图,侧视图均为矩形,俯视图为等腰直角三角形,则该几何体的体积为 已知一几何体的三视图如图,主视图和左视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,以这4个点为顶点的几何形体可能是( )
已知一几何体的三视图如图,主视图和左视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,以这4个点为顶点的几何形体可能是( ) 已知一几何体的三视图如图,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值.
已知一几何体的三视图如图,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值.