写出命题:“已知x∈R.若x=2或x=-3.则=0 的逆命题.否命题和逆否命题.并判断它们和原命题的真假．题目和参考答案——青夏教育精英家教网—

题目内容

11．写出命题：“已知x∈R，若x=2或x=-3，则（x-2）（x+3）=0”的逆命题、否命题和逆否命题，并判断它们和原命题的真假．

分析根据四种命题之间的关系，分别写出它们的逆命题、否命题和逆否命题，并判断它们的真假．

解答解：原命题：“已知x∈R，若x=2或x=-3，则（x-2）（x+3）=0，是真命题；
逆命题：已知x∈R，若（x-2）（x+3）=0，则x=2或x=-3，是真命题；
否命题：已知x∈R，若x≠2且x≠-3，则（x-2）（x+3）≠0，是真命题；
逆否命题：已知x∈R，若（x-2）（x+3）≠0，则x≠2且x≠-3，是真命题．

点评本题考查了四种命题之间的关系，也考查了命题真假的判断问题，是基础题目．

练习册系列答案

2．已知数列{a_n}是公差不为零的等差数列，a₁=1，且a₁，a₃，a₉成等比数列．
（1）求数列{a_n}的通项公式；
（2）若b_n=2^a_n+a_n，求数列{b_n}的前n项和S_n．

19．已知数列{a_n}的前n项和S_n，a₁=1，且a_n=-S_n-1（n∈N^*）．
（1）求证：数列{a_n}是等比数列；
（2）设b_n=$\frac{6}{lo{g}_{2}{a}_{n+1}•lo{g}_{2}{a}_{n+2}}$，求数列{b_n}前n项和T_n．

6．已知函数$f（x）=\left\{\begin{array}{l}ax，\;x≥0\\ 1-x，x＜0\end{array}\right.（a∈R）$，若f[f（-1）]=2，则a=（　　）

16．已知函数f（x）=|x-a|．
（1）若不等式f（x）≤3的解集为{x|b≤x≤5}，求a+b的值；
（2）在（1）的条件下，若f（x）+f（x+5）≥m对一切实数x恒成立，求实数m的取值范围．

3．已知函数f（x）=$\frac{{x}^{2}+2x+\frac{1}{a}}{x}$（a＞0）
（1）当a=2时，试判断x∈[1，+∞）它的单调性
（2）若x∈（0，1]时，f（x）是减函数，x∈[1，+∞）时，f（x）是增函数，试求a的值及x∈（0，+∞）上f（x）的最小值．

20．已知a、b表示两条不同的直线，α，β表示两个不同的平面，则下列命题正确的是（　　）

	A．	若α∥β，a∥α，b∥β，则a∥b		B．	若a?α，b?β，a∥b，则α∥β
	C．	若a⊥α，b⊥β，α⊥β，则a∥b		D．	若a⊥α，b⊥β，a⊥b，则α⊥β

1．

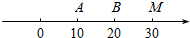如图，O为数轴的原点，A，B，M为数轴上三点，C为线段OM上的动点，设x表示C与原点的距离，y表示C到A的距离4倍与C到距离的6倍的和．
（Ⅰ）将y表示为x的函数；
（Ⅱ）要使y的值不超过70，x应该在什么范围内取值？

试题分类