题目内容
设O是平行四边形ABCD的两条对角线的交点，下列向量组：
（1）
与
；
（2）
与
；
（3）
与
；
（4）
与
，
其中可作为这个平行四边形所在平面表示它的所有向量的基底的向量组可以是
（1）
| AD |
| AB |
（2）
| DA |
| BC |
（3）
| CA |
| DC |
（4）
| OD |
| OB |
其中可作为这个平行四边形所在平面表示它的所有向量的基底的向量组可以是
（1），（3）
（1），（3）
．分析：要向量组可作为这个平行四边形所在平面表示它的所有向量的基底，这两个向量必不共线（平行），画出图形，利用图象分析向量之间是否共线后，可得答案．
解答：解：如下图所示：
（1）
与
不共线，故（1）可作为这个平行四边形所在平面表示它的所有向量的基底；
（2）
与
共线，故（2）不可作为这个平行四边形所在平面表示它的所有向量的基底；
（3）
与
不共线，故（3）可作为这个平行四边形所在平面表示它的所有向量的基底；
（4）
与
共线，故（4）不可作为这个平行四边形所在平面表示它的所有向量的基底；
故答案为：（1），（3）
（1）
| AD |
| AB |
（2）
| DA |
| BC |
（3）
| CA |
| DC |
（4）
| OD |
| OB |
故答案为：（1），（3）
点评：本题又命题的真假判断为载体考查了平面向量的基本定理，熟练掌握基底的定义是解答的关键．
练习册系列答案
精英口算卡系列答案
相关题目
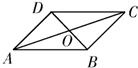如图，设O是平行四边形ABCD的两条对角线AC，BD的交点，下列向量组：