Question

（本小题满分12分）

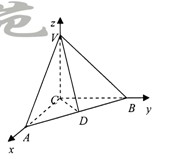
       如图，△VAC中，，将其绕直线VC旋转得到△VBC，D是AB的中点，

   （Ⅰ）求证：平面VAB⊥平面VCD；

   （Ⅱ）当角θ变化时，求直线BC与平面VAB所成的角的取值范围.

   （Ⅲ）当时，在线段VB上能否找到点E使二面角E—CD—B的大小为，若能，求；若不能，说明理由。

Answer 1

解：（Ⅰ）∵

∴AC⊥BC，

∵，，

∴VC⊥平面ABC，

以C为坐标原点，CA、CB、CV为x、y、z轴建立坐标系如图，则

A（a,0,0）,B(0,a,0),D(,,0)，V（0，0，），

∴=(,,－)，(,,0)， (－a,a,0),

∴,,

∴AB⊥平面VCD,

∵AB平面VAB，

∴平面VAB⊥平面VCD，

（Ⅱ）设平面VAB的法向量为，

∴，

，

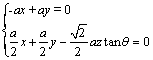∴，又，

设直线BC与平面VAB所成角为，

∴，

∵，∴，

∴，

（Ⅲ）当时，V（0，0，），

假设存在点E，则，

∴，

设平面CDE的法向量为，

∴，

∴，

∴，

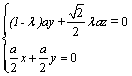∵二面角E—CD—B的大小为，

∴，

∴，∴，

故符合题意的.