题目内容
2．当x＞0时，若不等式x2+ax+1≥0恒成立，则a的最小值为（ ）| A． | -2 | B． | -3 | C． | -1 | D． | $-\frac{3}{2}$ |
分析 不等式对应的二次函数的二次项系数大于0，对应的图象是开口向上的抛物线，当判别式小于等于0时，不等式对任意实数恒成立，当判别式大于0时，需对称轴在直线x=0的左侧，当x=0时对应的函数式的值大于等于0，由此列式可求得实数a的取值范围．
解答 解：当△=a2-4≤0，即-2≤a≤2时，不等式x2+ax+1≥0对任意x＞0恒成立，
当△=a2-4＞0，则需$\left\{\begin{array}{l}{{a}^{2}-4＞0}\\{-\frac{a}{2}＜0}\end{array}\right.$，
解得a＞2．
所以使不等式x2-2ax+1≥0对任意x＞0恒成立的实数a的最小值是-2．
故选：A．
点评 本题考查一元二次不等式的解法，考查分类讨论的思想方法，训练了“三个二次”结合处理有关问题，是中档题．
练习册系列答案
应用题作业本系列答案
相关题目
12．
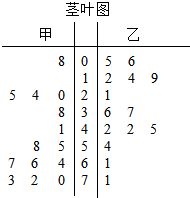为了调查甲、乙两个网站受欢迎的程度，随机选取了14天，统计上午8：00-10：00间各自的点击量，得到如图茎叶图，则甲、乙两个网站点击量的中位数分别是（ ）
为了调查甲、乙两个网站受欢迎的程度，随机选取了14天，统计上午8：00-10：00间各自的点击量，得到如图茎叶图，则甲、乙两个网站点击量的中位数分别是（ ）| A． | 55，36 | B． | 55.5，36.5 | C． | 56.5，36.5 | D． | 58，37 |
7．设复数z1=2-i，z2=1-3i，则复数$\frac{i}{{z}_{1}}$+$\frac{\overline{{z}_{2}}}{5}$的虚部等于（ ）
| A． | 1 | B． | -1 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
14．数列$1\frac{1}{2}，2\frac{1}{4}，3\frac{1}{8}，4\frac{1}{16}，…$的通项公式an可以是（ ）
| A． | ${a_n}=n+\frac{1}{2^n}$ | B． | ${a_n}=n•\frac{1}{2^n}$ | C． | ${a_n}=n+\frac{1}{{{2^{n-1}}}}$ | D． | ${a_n}=（{n-1}）+\frac{1}{{{2^{n-1}}}}$ |