题目内容
已知双曲线C的方程为 -
-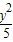 =1,若直线x-my-3=0截双曲线的一支所得弦长为5.
=1,若直线x-my-3=0截双曲线的一支所得弦长为5.(I)求m的值;
(II)设过双曲线C上的一点P的直线与双曲线的两条渐近线分别交于P1,P2,且点P分有向线段
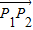 所成的比为λ(λ>0).当
所成的比为λ(λ>0).当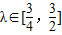 时,求|
时,求|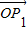 ||
||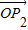 |(O为坐标原点)的最大值和最小值.
|(O为坐标原点)的最大值和最小值.
【答案】分析:(I)由直线x-my-3=0可知:直线恒过定点焦点F2(3,0).于是直线与双曲线的右支相交,设两点分别为A(x1,y1),B(x2,y2).由双曲线的第二定义可得: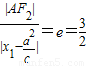 ,即
,即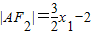 ,同理
,同理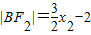 .于是|AB|=|AF2|+|BF2|=
.于是|AB|=|AF2|+|BF2|=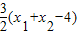 ,由题意可得:
,由题意可得: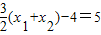 ,由直线过焦点F2(3,0),可知x1=x2=3,此时直线垂直于x轴,即可得出m的值.
,由直线过焦点F2(3,0),可知x1=x2=3,此时直线垂直于x轴,即可得出m的值.
(II)利用线段的定比分点坐标公式即可得出点P的坐标用P1,P2的坐标表示,代入双曲线的方程即可得出x1x2,进而得出| ||
||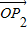 |的最值.
|的最值.
解答:解:(I)由双曲线C的方程为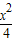 -
-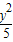 =1可得a=2,
=1可得a=2,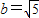 ,
,
∴c=3,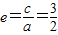 .
.
左右焦点分别为F1(-3,0),F2(3,0).
由直线x-my-3=0可知:直线恒过定点焦点F2(3,0).
于是直线与双曲线的右支相交,设两点分别为A(x1,y1),B(x2,y2).
由双曲线的第二定义可得: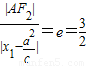 ,即
,即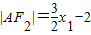 ,同理
,同理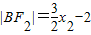 .
.
∴|AB|=|AF2|+|BF2|=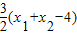 ,由题意可得:
,由题意可得: ,∴|x1+x2|=6,
,∴|x1+x2|=6,
由直线过焦点F2(3,0),可知x1=x2=3,
此时直线垂直于x轴,∴m=0.
(II)双曲线C的渐近线方程分别为l1: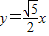 ,l2:
,l2: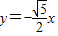 .
.
设P(x,y),P1(x1,y1),P2(x2,y2).
且点P分有向线段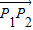 所成的比为λ(λ>0).
所成的比为λ(λ>0).
则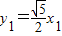 ,
,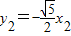 ,
,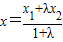 ,
, .
.
由点P(x,y)在双曲线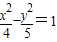 上,∴
上,∴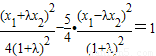 ,
,
化简得 ,又
,又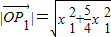 =
= ,同理可得:
,同理可得: ,
,
∴ ,
,
令u(x)=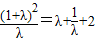 ,
,
又u(λ)在(0,1]上单调递减,在[1,+∞)上单调递增,而λ∈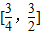 ,
,
∴u(λ)min=u(1)=4,u(λ)max=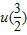 =
=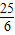 .
.
于是: 的最大值为
的最大值为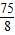 ,最小值为9.
,最小值为9.
点评:熟练掌握双曲线的标准方程及其性质、线段的定比分点坐标公式、函数的单调性等是解题的关键.
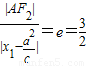 ,即
,即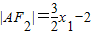 ,同理
,同理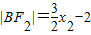 .于是|AB|=|AF2|+|BF2|=
.于是|AB|=|AF2|+|BF2|=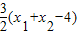 ,由题意可得:
,由题意可得: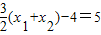 ,由直线过焦点F2(3,0),可知x1=x2=3,此时直线垂直于x轴,即可得出m的值.
,由直线过焦点F2(3,0),可知x1=x2=3,此时直线垂直于x轴,即可得出m的值.(II)利用线段的定比分点坐标公式即可得出点P的坐标用P1,P2的坐标表示,代入双曲线的方程即可得出x1x2,进而得出|
 ||
||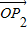 |的最值.
|的最值.解答:解:(I)由双曲线C的方程为
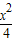 -
-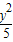 =1可得a=2,
=1可得a=2,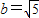 ,
,∴c=3,
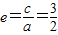 .
.左右焦点分别为F1(-3,0),F2(3,0).
由直线x-my-3=0可知:直线恒过定点焦点F2(3,0).
于是直线与双曲线的右支相交,设两点分别为A(x1,y1),B(x2,y2).
由双曲线的第二定义可得:
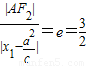 ,即
,即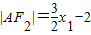 ,同理
,同理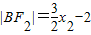 .
.∴|AB|=|AF2|+|BF2|=
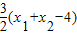 ,由题意可得:
,由题意可得: ,∴|x1+x2|=6,
,∴|x1+x2|=6,由直线过焦点F2(3,0),可知x1=x2=3,
此时直线垂直于x轴,∴m=0.
(II)双曲线C的渐近线方程分别为l1:
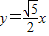 ,l2:
,l2: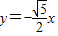 .
.设P(x,y),P1(x1,y1),P2(x2,y2).
且点P分有向线段
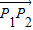 所成的比为λ(λ>0).
所成的比为λ(λ>0).则
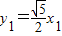 ,
,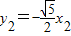 ,
,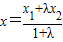 ,
, .
.由点P(x,y)在双曲线
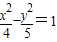 上,∴
上,∴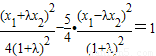 ,
,化简得
 ,又
,又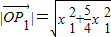 =
= ,同理可得:
,同理可得: ,
,∴
 ,
,令u(x)=
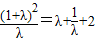 ,
,又u(λ)在(0,1]上单调递减,在[1,+∞)上单调递增,而λ∈
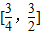 ,
,∴u(λ)min=u(1)=4,u(λ)max=
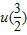 =
=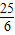 .
.于是:
 的最大值为
的最大值为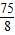 ,最小值为9.
,最小值为9.点评:熟练掌握双曲线的标准方程及其性质、线段的定比分点坐标公式、函数的单调性等是解题的关键.

练习册系列答案
相关题目