题目内容
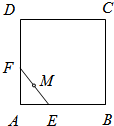 如图,设线段EF的长度为1,端点E、F在边长为2的正方形ABCD的四边上滑动.当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G围成的面积为S,则S=
如图,设线段EF的长度为1,端点E、F在边长为2的正方形ABCD的四边上滑动.当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G围成的面积为S,则S=分析:以A为原点,AB,AD所在直线分别为x,y轴建立平面直角坐标系,求出G在A角处的轨迹,从而得到G的轨迹围成的图形是正方形挖去四个四分之一圆周,由正方形的面积减去圆的面积得答案.
解答:解:假设正方形的拐角的点A为坐标原点(0,0),
再设点E的坐标是(x′,0),点F(0,y′),中点M(x,y)
则x=
,y=
,即x′=2x,y′=2y.
因为EF距离为1,即(x′)2+(y′)2=1
把x′=2x,y′=2y代入之后,得到x2+y2=
.
∵x′在0到1,∴画出图象只有一段圆弧.
这段圆弧位于圆心在(0,0),半径为
的圆上,而且是圆周长的
.
∴四部分的圆弧加起来就是整个圆了.
面积为π×(
)2=
.
∴G围成的面积为S等于正方形的面积减去
.即为4-
.
故答案为:4-
.
再设点E的坐标是(x′,0),点F(0,y′),中点M(x,y)
则x=
| x′ |
| 2 |
| y′ |
| 2 |
因为EF距离为1,即(x′)2+(y′)2=1
把x′=2x,y′=2y代入之后,得到x2+y2=
| 1 |
| 4 |
∵x′在0到1,∴画出图象只有一段圆弧.
这段圆弧位于圆心在(0,0),半径为
| 1 |
| 2 |
| 1 |
| 4 |
∴四部分的圆弧加起来就是整个圆了.
面积为π×(
| 1 |
| 2 |
| π |
| 4 |
∴G围成的面积为S等于正方形的面积减去
| π |
| 4 |
| π |
| 4 |
故答案为:4-
| π |
| 4 |
点评:本题考查了轨迹方程,考查了封闭曲线面积的求法,关键是求出正方形四个角处的G的轨迹,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (1)(如图1)在边长为4的正方形ABCD中,E、F分别是边AB,BC上的点,且AE=BF=1,过线段EF上的点P分别作DC,AD的垂线,垂足为M,N,延长NP交BC于Q,试写出矩形PMDN的面积y与FQ的长x之间的函数关系,并求出y的最大值.
(1)(如图1)在边长为4的正方形ABCD中,E、F分别是边AB,BC上的点,且AE=BF=1,过线段EF上的点P分别作DC,AD的垂线,垂足为M,N,延长NP交BC于Q,试写出矩形PMDN的面积y与FQ的长x之间的函数关系,并求出y的最大值.
 (λ>O,λ为变量)
(λ>O,λ为变量)
 ,P(0,0,2).
,P(0,0,2).
 ,
, 于是
于是 ,所以
,所以
 设平面PCD的法向量
设平面PCD的法向量 ,
, ,即
,即 .不防设
.不防设 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量 于是
于是 从而
从而 .
. .
. ,由此得
,由此得 .
.
 ,解得
,解得 ,即
,即 .
. ,可得
,可得 ,又由
,又由 ,
, ,故
,故 .又
.又 ,所以
,所以
 于点H,连接DH.由
于点H,连接DH.由 ,可得
,可得 .
. ,从而
,从而 为二面角A-PC-D的平面角.在
为二面角A-PC-D的平面角.在 中,
中, ,由此得
,由此得 由(1)知
由(1)知 ,故在
,故在 中,
中,
 所以二面角
所以二面角 的正弦值为
的正弦值为 ,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故
,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故 或其补角为异面直线BE与CD所成的角.由于BF∥CD,故
或其补角为异面直线BE与CD所成的角.由于BF∥CD,故 .在
.在 中,
中, 故
故

 中,由
中,由 ,
, ,
,
 .由余弦定理,
.由余弦定理, ,
, 的长为2,宽为1,
的长为2,宽为1, 边分别在x轴、y轴的正半轴上,
边分别在x轴、y轴的正半轴上, 点与坐标原点重合(如图4所示),将矩形折叠,使
点与坐标原点重合(如图4所示),将矩形折叠,使 上.
上. ,试写出折痕所在直线的方程;
,试写出折痕所在直线的方程; , 求
, 求 的解析式.
的解析式.