题目内容
设不等式组
|
(1)求f(1),f(2)的值及f(n)的表达式;
(2)记Tn=
| f(n)•f(n+1) |
| 2n |
(3)设Sn为数列bn的前n项的和,其中bn=2f(n),问是否存在正整数n,t,使
| Sn+tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |
分析:(1)直接把n=1,2代入即可求出f(1),f(2)的值;再把x=1,x=2代入综合求出f(n)的表达式;
(2)先利用上面的结论求出Tn的表达式,再对Tn与Tn+1的作商比较,从而求出Tn中的最大值,即可找到满足Tn≤m时对应的实数m的取值范围;
(3)先利用bn=2f(n)求出数列{bn}的通项公式,进而求出Sn;把Sn代入
<
,化简得
<
,再分t=1以及t>1求出其对应的n即可说明结论.
(2)先利用上面的结论求出Tn的表达式,再对Tn与Tn+1的作商比较,从而求出Tn中的最大值,即可找到满足Tn≤m时对应的实数m的取值范围;
(3)先利用bn=2f(n)求出数列{bn}的通项公式,进而求出Sn;把Sn代入
| Sn+tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |
(
| ||||
(
|
| 1 |
| 2 |
解答:解:(1)f(1)=3,f(2)=6(2分)
当x=1时,y取值为1,2,3,…,2n共有2n个格点
当x=2时,y取值为1,2,3,…,n共有n个格点
∴f(n)=n+2n=3n(4分)
(2)由Tn=
=
则Tn+1=
=
?
=
=
(5分)
当n=1,2时,Tn+1≥Tn
当n≥3时,n+2<2n?Tn+1<Tn(6分)
∴n=1时,T1=9n=2,3时,T2=T3=
n≥4时,Tn<T3
∴Tn中的最大值为T2=T3=
(8分)
要使Tn≤m对于一切的正整数n恒成立,
只需
≤m
∴m≥
(9分)
(3)bn=2f(n)=23n=8 n?Sn=
=
(8 n-1)(10分)
将Sn代入
<
,化简得,
<
(﹡)(11分)
若t=1时,
<
?8n<
,显然不成立,
若t>1时,(﹡)式化简为(
-t)8n>
不可能成立,
综上,不存在正整数n,t使
<
成立.
当x=1时,y取值为1,2,3,…,2n共有2n个格点
当x=2时,y取值为1,2,3,…,n共有n个格点
∴f(n)=n+2n=3n(4分)
(2)由Tn=
| f(n)f(n+1) |
| 2n |
| 9n(n+1) |
| 2n |
则Tn+1=
| f(n+1)f(n+2) |
| 2n+1 |
| 9(n+1)(n+2) |
| 2n+1 |
| Tn+1 |
| Tn |
| ||
|
| n+2 |
| 2n |
当n=1,2时,Tn+1≥Tn
当n≥3时,n+2<2n?Tn+1<Tn(6分)
∴n=1时,T1=9n=2,3时,T2=T3=
| 27 |
| 2 |
∴Tn中的最大值为T2=T3=
| 27 |
| 2 |
要使Tn≤m对于一切的正整数n恒成立,
只需
| 27 |
| 2 |
∴m≥
| 27 |
| 2 |
(3)bn=2f(n)=23n=8 n?Sn=
| 8(1-8n) |
| 1-8 |
| 8 |
| 7 |
将Sn代入
| Sn+tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |
(
| ||||
(
|
| 1 |
| 16 |
若t=1时,
| ||||
|
| 1 |
| 16 |
| 15 |
| 29 |
若t>1时,(﹡)式化简为(
| 8 |
| 7 |
| 15 |
| 7 |
综上,不存在正整数n,t使
| Sn+tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |
点评:本题综合考查了数列,函数以及不等式,是对知识点的综合考查.解决本题的关键点在于求出f(n)的表达式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
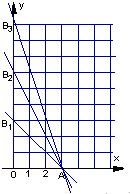 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组