题目内容
(12分)已知定义域为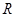 的偶函数
的偶函数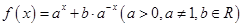 .
.
(1)求实数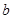 的值;
的值;
(2)判断并证明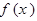 的单调性;
的单调性;
(3)若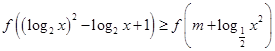 对任意
对任意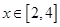 恒成立,求实数
恒成立,求实数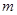 的取值范围.
的取值范围.
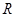 的偶函数
的偶函数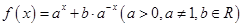 .
. (1)求实数
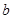 的值;
的值; (2)判断并证明
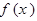 的单调性;
的单调性;(3)若
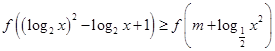 对任意
对任意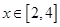 恒成立,求实数
恒成立,求实数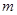 的取值范围.
的取值范围. (1)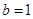 ;
;
(2)设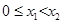 ,则
,则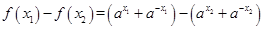
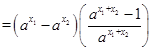
当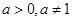 时,
时,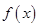 为
为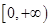 上的增函数;当
上的增函数;当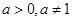 时,
时,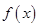 为
为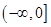 上的减函数。(3)
上的减函数。(3)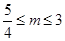 。
。
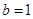 ;
;(2)设
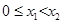 ,则
,则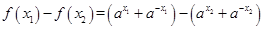
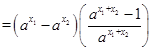
当
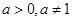 时,
时,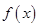 为
为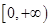 上的增函数;当
上的增函数;当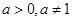 时,
时,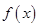 为
为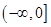 上的减函数。(3)
上的减函数。(3)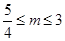 。
。试题分析:(1)
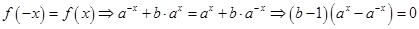
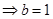 …… ……………………………………………3分
…… ……………………………………………3分⑵设
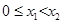
则
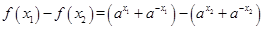
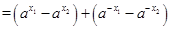
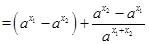
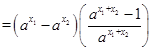
当
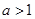 时,
时,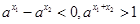 ,
,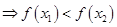 ,
,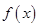 为
为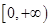 上的增函数;
上的增函数;当
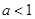 时,
时,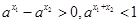 ,
,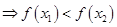 ,
,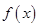 为
为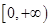 上的增函数。
上的增函数。综上可得,当
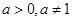 时,
时,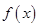 为
为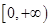 上的增函数。
上的增函数。同理可证,当
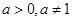 时,
时,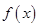 为
为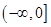 上的减函数。 ………………7分
上的减函数。 ………………7分⑶
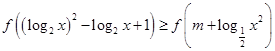 对任意
对任意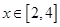 恒成立,
恒成立,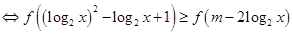 对任意
对任意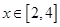 恒成立,
恒成立,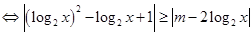 对任意
对任意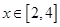 恒成立,
恒成立,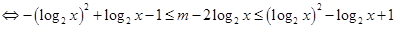 对任意
对任意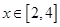 恒成立
恒成立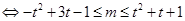 对任意
对任意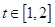 恒成立,(令
恒成立,(令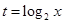 )
)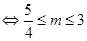 ……………………………………12分
……………………………………12分点评:用定义法证明函数单调性的步骤:一设二作差三变形四判断符号五得出结论,其中最重要的是四变形,最好变成几个因式乘积的形式,这样便于判断符号。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
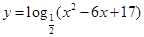 的值域是 .
的值域是 .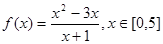 的值域是( )
的值域是( )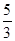 ]
]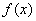 的定义域为
的定义域为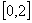 ,则
,则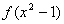 的定义域为______ ___;
的定义域为______ ___;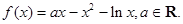
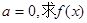 的单调区间;
的单调区间;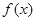 存在极值,且所有极值之和大于
存在极值,且所有极值之和大于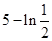 ,求a的取值范围。
,求a的取值范围。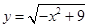 的值域为( )
的值域为( )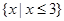



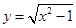 的定义域是 。
的定义域是 。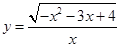 的定义域为 ( )
的定义域为 ( )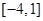
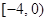

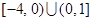
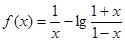 。
。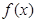 的定义域;
的定义域;