题目内容
在平面直角坐标系中,△ABC的两个顶点A、B的坐标分别是(-1,0),(1,0),点G是△ABC的重心,y轴上一点M满足GM∥AB,且|MC|=|MB|.(I)求△ABC的顶点C的轨迹E的方程;
(II)不过点A的直线l:y=kx+b与轨迹E交于不同的两点P、Q,当
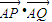 =0时,求k与b的关系,并证明直线l过定点.
=0时,求k与b的关系,并证明直线l过定点.
【答案】分析:(I)先设出点C的坐标,利用G为△ABC的重心找到点G的坐标,再利用点M在y轴上且MG∥AB求出点M的坐标,结合∵|MC|=|MB|即可找到△ABC的顶点C的轨迹E的方程;
(II)先把直线方程和轨迹E的方程联立找到关于点P和点Q坐标之间的关系式,再利用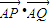 =0就可找到k与b的关系,再反代入直线方程,就可证明直线l过定点.
=0就可找到k与b的关系,再反代入直线方程,就可证明直线l过定点.
解答:解:(I)设点C坐标为(x,y)
因为G为△ABC的重心
故G点坐标为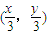 (2分)
(2分)
由点M在y轴上且MG∥AB知点M的坐标为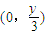 ∵|MC|=|MB|∴
∵|MC|=|MB|∴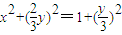 ,
,
即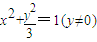
∴△ABC的顶点C的轨迹E的方程是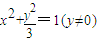 (5分)
(5分)
(II)设直线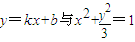 的两交点为P(x1,y1),Q(x2,y2)
的两交点为P(x1,y1),Q(x2,y2)
把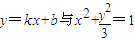 联立得:
联立得: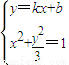
消去y得:(k2+3)x2+2kbx+b2-3=0(7分)
∴△=4k2b2-4(k2+3)(b2-3)=12(k2-b2+3)>0
且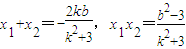 .(9分)
.(9分)
∵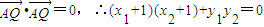
故(k2+1)x1x2+(kb+1)(x1+x2)+b2=0
代入整理得:k2+kb-2b2=0∴k=b或k=-2b.(10分)
(1)当k=b时,y=kx+b=k(x+1)直线过点(-1,0)不合题意舍去.
(2)当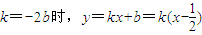 ,直线过点
,直线过点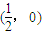
综上知:k=-2b,直线过定点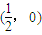 (14分)
(14分)
点评:本题综合考查了直线与椭圆的位置关系以及向量垂直问题.在做第一问时,一定要注意点C不能与AB在一条直线上.
(II)先把直线方程和轨迹E的方程联立找到关于点P和点Q坐标之间的关系式,再利用
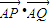 =0就可找到k与b的关系,再反代入直线方程,就可证明直线l过定点.
=0就可找到k与b的关系,再反代入直线方程,就可证明直线l过定点.解答:解:(I)设点C坐标为(x,y)
因为G为△ABC的重心
故G点坐标为
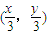 (2分)
(2分)由点M在y轴上且MG∥AB知点M的坐标为
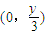 ∵|MC|=|MB|∴
∵|MC|=|MB|∴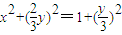 ,
,即
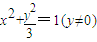
∴△ABC的顶点C的轨迹E的方程是
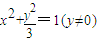 (5分)
(5分)(II)设直线
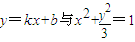 的两交点为P(x1,y1),Q(x2,y2)
的两交点为P(x1,y1),Q(x2,y2)把
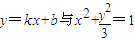 联立得:
联立得: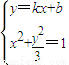
消去y得:(k2+3)x2+2kbx+b2-3=0(7分)
∴△=4k2b2-4(k2+3)(b2-3)=12(k2-b2+3)>0
且
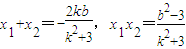 .(9分)
.(9分)∵
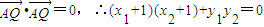
故(k2+1)x1x2+(kb+1)(x1+x2)+b2=0
代入整理得:k2+kb-2b2=0∴k=b或k=-2b.(10分)
(1)当k=b时,y=kx+b=k(x+1)直线过点(-1,0)不合题意舍去.
(2)当
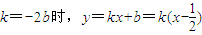 ,直线过点
,直线过点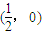
综上知:k=-2b,直线过定点
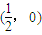 (14分)
(14分)点评:本题综合考查了直线与椭圆的位置关系以及向量垂直问题.在做第一问时,一定要注意点C不能与AB在一条直线上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目