��Ŀ����
����С������12�֣�
ij�����ƻ������ס������ֲ�Ʒ�������ֲ�Ʒ����Ҫ����ԭ�ϡ������ײ�Ʒ1��ʱ��ҪA��ԭ��3kg��B��ԭ��1 kg�������Ҳ�Ʒ1��ʱ��ҪA��ԭ��2kg��B��ԭ��2kg������A��ԭ��1200 kg��B��ԭ��800 kg����������ײ�Ʒÿ��ʱ��ƽ��������30Ԫ�������Ҳ�Ʒÿ��ʱ��ƽ��������40Ԫ���ʼס������ֲ�Ʒ���������ٹ�ʱ��ʹ������ܶ������������Ƕ��٣�
���𰸡�
�������ֲ�Ʒ200��ʱ���������ֲ�Ʒ300��ʱ����������ܶ����18000Ԫ
��������
���������.�⣺��ƻ��������ֲ�Ʒx��ʱ���������ֲ�Ʒy��ʱ�����������ܶ�Ϊ
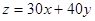
�������������ͼ

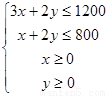
����ԭ���ֱ��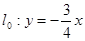 ��ƽ�ƾ����㣨200��300��ʱ�ݽؾ����
��ƽ�ƾ����㣨200��300��ʱ�ݽؾ����
���Ե�x=200��y=300ʱ��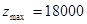
�����������ֲ�Ʒ200��ʱ���������ֲ�Ʒ300��ʱ����������ܶ����18000Ԫ
���㣺�����⿼�������Իع��ʵ��Ӧ�á�
���������������Ĺؼ���Ҫ�������⣬��ʵ������ת��Ϊ��ѧ���⣬���������ʽ�Ĺ�ϵ�������õ�����ʽ�飬���ͼ��������Իع��֪ʶ�������õ���ֵ���⣬���ڻ����⡣

��ϰ��ϵ�д�
�����Ŀ