题目内容
已知函数f（x）=|loga|x-1||（a＞0，a≠1），若x1＜x2＜x3＜x4，x1x2x3x4≠0且f（x1）=f（x2）=f（x3）=f（x4），则x1+x2+x3+x4=（ ）
| A、2 | B、4 | C、8 | D、随a值变化 |
考点：对数函数图象与性质的综合应用
专题：函数的性质及应用
分析：画出函数f（x）=|loga|x-1||的图象，分析函数的对称性，进而可得答案．
解答：解：函数f（x）=|loga|x-1||的图象如下图所示：
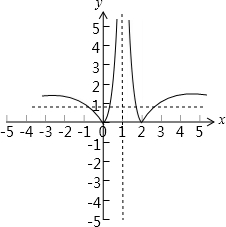
有图可知，函数f（x）=|loga|x-1||的图象关于直线x=1对称，
又∵x1＜x2＜x3＜x4，且f（x1）=f（x2）=f（x3）=f（x4），
则x1+x2+x3+x4=4．
故选：B
有图可知，函数f（x）=|loga|x-1||的图象关于直线x=1对称，
又∵x1＜x2＜x3＜x4，且f（x1）=f（x2）=f（x3）=f（x4），
则x1+x2+x3+x4=4．
故选：B
点评：本题考查的知识点是函数图象的对折变换，函数图象的对称性，其中根据已知分析出函数f（x）=|loga|x-1||的图象关于直线x=1对称，是解答的关键．
练习册系列答案
相关题目
已知集合A={x|log2x≥0}，B={x|x（x-2）≤0}，则（∁RA）∩B=（ ）
| A、[0，2] | B、（0，1） | C、[0，1） | D、（1，2] |
如果函数f（x）在[a，b]上的最大值和最小值分别为M、m，那么m（b-a）≤△
f（x）≤M（b-a）．根据这一结论求出△
2 -x2的取值范围（ ）
b a |
2 -1 |
| A、[0，3] | ||||
B、[
| ||||
C、[
| ||||
D、[
|
设a=30.2，b=(
)-1.1，c=log32，则a，b，c的大小关系是（ ）
| 1 |
| 3 |
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＜a＜b |
| D、c＜b＜a |
定义区间[x1，x2]的长度为x2-x1．若函数y=|log2x|的定义域为[a，b]，值域为[0，2]，则区间[a，b]的长度的最大值为（ ）
A、
| ||
B、
| ||
| C、3 | ||
D、
|
函数f（x）=x3-
的零点个数为（ ）
| 1 |
| x |
| A、0 | B、1 | C、2 | D、3 |
用二分法求方程lgx=3-x的近似解，可以取的一个区间是（ ）
| A、（0，1） | B、（1，2） | C、（2，3） | D、（3，4） |
定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈[0，2）时，f（x）=
若x∈[-4，-2）时，f（x）≤
-
有解，则实数t的取值范围是（ ）
|
| t |
| 4 |
| 1 |
| 2t |
| A、[-2，0）∪（0，1） |
| B、[-2，0）∪[1，+∞） |
| C、[-2，1] |
| D、（-∞，-2]∪（0，1] |