题目内容
已知函数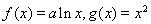 .其中
.其中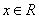 .
.
(1)若曲线y=f(x)与y=g(x)在x=1处的切线相互平行,求两平行直线间的距离;
(2)若f(x)≤g(x)-1对任意x>0恒成立,求实数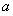 的值;
的值;
(3)当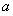 <0时,对于函数h(x)=f(x)-g(x)+1,记在h(x)图象上任取两点A、B连线的斜率为
<0时,对于函数h(x)=f(x)-g(x)+1,记在h(x)图象上任取两点A、B连线的斜率为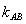 ,若
,若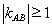 ,求
,求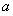 的取值范围.
的取值范围.
(1) ;(2)2; (3)
;(2)2; (3)
【解析】
试题分析:(1)因为曲线y=f(x)与y=g(x)在x=1处的切线相互平行,所以分别对这两个函数求导,可得导函数在x=1处的斜率相等,即可求出 的值以及求出两条切线方程.再根据平行间的距离公式求出两切线的距离.
的值以及求出两条切线方程.再根据平行间的距离公式求出两切线的距离.
(2) 由f(x)≤g(x)-1对任意x>0恒成立,所以构造一个新的函数,在x>0时求出函数的最值符合条件即可得到 的范围.
的范围.
(3)根据(2)所得的结论当当 <0时,由(2)知
<0时,由(2)知 <0,∴h(x)在(0,+∞)上是减函数,所以根据
<0,∴h(x)在(0,+∞)上是减函数,所以根据 可以得到函数与变量的关系式,从而构造一个新的函数,得到
可以得到函数与变量的关系式,从而构造一个新的函数,得到 的范围.
的范围.
试题解析:(1) ,依题意得:
,依题意得:  =2;
=2;
曲线y=f(x)在x=1处的切线为2x-y-2=0,
曲线y=g(x)在x=1处的切线方程为2x-y-1=0.两直线间的距离为
(2)令h(x)=f(x)-g(x)+1, ,则
当 ≤0时, 注意到x>0, 所以
≤0时, 注意到x>0, 所以 <0, 所以h(x)在(0,+∞)单调递减,又h(1)=0,故0<x<1时,h(x)>0,即f(x)> g(x)-1,与题设矛盾.
<0, 所以h(x)在(0,+∞)单调递减,又h(1)=0,故0<x<1时,h(x)>0,即f(x)> g(x)-1,与题设矛盾.
当 >0时,
>0时,
当 ,
, 当
当 时,
时,
所以h(x)在上是增函数,在上是减函数,
∴h(x)≤
因为h(1)=0,又当 ≠2时,≠1,
≠2时,≠1, 与
与 不符.所以
不符.所以 =2.
=2.
(3)当 <0时,由(2)知
<0时,由(2)知 <0,∴h(x)在(0,+∞)上是减函数,
<0,∴h(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|h(x1)-h(x2)|=h(x1)-h(x2),|x1-x2|=x2-x1,
∴|h(x1)-h(x2)|≥|x1-x2|
等价于h(x1)-h(x2)≥x2-x1,即h(x1)+x1≥h(x2)+x2,令H(x)=h(x)+x= lnx-x2+x+1,H(x)在(0,+∞)上是减函数,
lnx-x2+x+1,H(x)在(0,+∞)上是减函数,
∵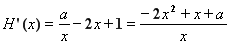 (x>0),∴-2x2+x+
(x>0),∴-2x2+x+ ≤0在x>0时恒成立,∴
≤0在x>0时恒成立,∴ ≤(2x2-x)min又x>0时, (2x2-x)min=
≤(2x2-x)min又x>0时, (2x2-x)min=
∴a≤-,又a<0,∴a的取值范围是 .
.
考点:1.导数的几何意义.2.含参数的不等式恒成立问题.3.函数方程间的等价变化转化为熟悉的问题从而解决问题.

 其中常数
其中常数 .
. 时,求函数
时,求函数 的单调递增区间;
的单调递增区间; 时,若函数
时,若函数 有三个不同的零点,求m的取值范围;
有三个不同的零点,求m的取值范围; 在点
在点 处的切线方程为
处的切线方程为 当
当 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数 是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由. 其中常数
其中常数
 时,求函数
时,求函数 的单调递增区间;
的单调递增区间; 时,给出两类直线:
时,给出两类直线: 与
与 ,其中
,其中 为常数,判断这两类直线中是否存在
为常数,判断这两类直线中是否存在 的切线,若存在,求出相应的
的切线,若存在,求出相应的 或
或 的值,若不存在,说明理由.
的值,若不存在,说明理由. 上的函数
上的函数 在点
在点 处的切线方程为
处的切线方程为 ,当
,当 若
若 在
在 为函数
为函数 其中实数
其中实数 。
。 在点
在点 处的切线方程;
处的切线方程;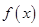 的单调性。
的单调性。