题目内容
(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知函数![]() 的反函数.定义:若对给定的实数
的反函数.定义:若对给定的实数![]() ,函数
,函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足“
满足“![]() 和性质”;若函数
和性质”;若函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足“
满足“![]() 积性质”.
积性质”.
(1) 判断函数![]() 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2) 求所有满足“2和性质”的一次函数;
(3) 设函数![]() 对任何
对任何![]() ,满足“
,满足“![]() 积性质”.求
积性质”.求![]() 的表达式.
的表达式.
(1)函数![]() 的反函数是
的反函数是![]() ,
,
![]()
![]() ,
,
而![]() ,其反函数为
,其反函数为![]()
故函数![]() 不满足“1和性质” …… 4分
不满足“1和性质” …… 4分
(2)设函数![]() 满足“2和性质”,
满足“2和性质”,![]() .
.
![]()
![]() ,
,![]()
![]() …… 6分
…… 6分
而![]() ,得反函数
,得反函数![]() , …… 8分
, …… 8分
由“2和性质”定义可知![]() 对
对![]() 恒成立.
恒成立.
![]()
![]() 即所求一次函数
即所求一次函数![]() . ……10分
. ……10分
(3)设![]() 且点
且点![]() 图像上,则
图像上,则![]() 在函数
在函数
![]() 图像上,
图像上,
故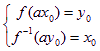 可得
可得![]() , ……12分
, ……12分
令![]() ,
,![]()
![]() . ……14分
. ……14分
综上所述,![]() 此时
此时![]() 其反函数是
其反函数是![]() ,
,
而![]() 故
故![]() 互为反函数. ……16分
互为反函数. ……16分
解析:
⑴分别求出![]() 的反函数和
的反函数和![]() ,然后对照,如果解析式相同,就满足“1和性质”,否则,不满足;
,然后对照,如果解析式相同,就满足“1和性质”,否则,不满足;
⑵知道函数的类型为一次函数,可用待定系数法设出函数解析式,因为满足“2和性质”,建立方程,求出参数的值;
⑶设出函数图象上任意一点A,根据反函数的性质,A关于直线y=x对称的点在其反函数图象上,进行计算和代换.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的