题目内容
已知函数f(x)=|ax-1|-2a(a>0,且a≠1)有两个零点,则a的取值范围是______.
设函数f(x)=|ax-1|-2a=0即|ax-1|=2a.
函数f(x)=|ax-1|-2a(a>0,且a≠1)有两个零点,即函数y=|ax-1|(a>0,且a≠1)与函数y=2a的图象有两个交点,
由图象可知当0<2a<1时两函数时,一定有两个交点.
所以实数a的取值范围是{a|0<a<
}.
故答案为:(0,
).
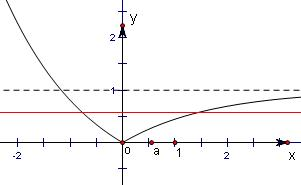
函数f(x)=|ax-1|-2a(a>0,且a≠1)有两个零点,即函数y=|ax-1|(a>0,且a≠1)与函数y=2a的图象有两个交点,
由图象可知当0<2a<1时两函数时,一定有两个交点.
所以实数a的取值范围是{a|0<a<
| 1 |
| 2 |
故答案为:(0,
| 1 |
| 2 |


练习册系列答案
相关题目









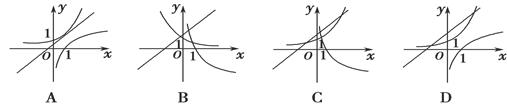
 的图象大致是( ).
的图象大致是( ).
 中,点
中,点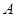 (2,1),
(2,1),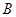 (3,0),点
(3,0),点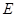 在射线
在射线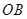 上自
上自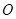 开始移动.设
开始移动.设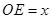 ,过
,过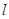 l,记△
l,记△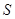 ,则函数
,则函数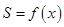 的图象是( )
的图象是( )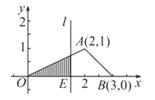
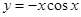 的部分图象是( )
的部分图象是( )