题目内容
如图10-23,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
图10-23
(Ⅰ)求截面EAC的面积;
(Ⅱ)求异面直线A1B1与AC之间的距离;
(Ⅲ)求三棱锥B1-EAC的体积.
(Ⅰ)解:如图10-55,连结DB交AC于O,连结EO.
∵底面ABCD是正方形,

图10-55
∴DO⊥AC 又∵ED⊥底面AC, ∴EO⊥AC.
∴∠EOD是面EAC与底面AC所成二面角的平面角,
∴∠EOD=45°
DO=![]() a,AC=
a,AC=![]() a,EO=
a,EO=![]() a·sec45°=a,
a·sec45°=a,
故S△EAC=![]() a2.
a2.
(Ⅱ)解:由题设ABCD-A1B1C1D1是正四棱柱,得A1A⊥底面AC,A1A⊥AC.
又A1A⊥A1B1,
∴A1A是异面直线A1B1与AC间的公垂线.
∵D1B∥面EAC,且面D1BD与面EAC交线为EO,
∴D1B∥EO又O是DB的中点.
∴E是D1D的中点,D1B=2EO=2a.
∴D1D=![]() =
=![]() a异面直线A1B1与AC间的距离为
a异面直线A1B1与AC间的距离为![]() a.
a.
(Ⅲ)方法一:如图10-56,连结D1B1.
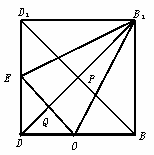
图10-56
∵D1D=DB=![]() a,
a,
∴BDD1B1是正方形连结B1D交D1B于P,交EO于Q
∵B1D⊥D1B,EO∥D1B,∴B1D⊥EO.
又AC⊥EO,AC⊥ED.
∴AC⊥面BDD1B1,∴B1D⊥AC,
∴B1D⊥面EAC.∴B1Q是三棱锥B1-EAC的高.
由DQ=PQ,得B1Q=![]() B1D=
B1D=![]() a
a
∴VB1-EAC=![]() ·
·![]() a2·
a2·![]() a=
a=![]() a3.
a3.
所以三棱锥B1-EAC的体积是![]() a3.
a3.
方法二:连结B1O,则VB1-EAC=2VA-EOB1
∵AO⊥面BDD1B1,
∴AO是三棱锥A-EOB1的高,AO=![]() a
a
在正方形BDD1B1中,E、O分别是D1D、DB的中点(如图10-56),则S△EOB1=![]() a2
a2
∴VB1-EAC=2·![]() ·
·![]() a2·
a2·![]() a=
a=![]() a3.
a3.
所以三棱锥B1-EAC的体积是![]() a3.
a3.

 (2013•昌平区一模)已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的全面积为( )
(2013•昌平区一模)已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的全面积为( )
 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC, (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,