题目内容
13. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )| A. | 在棱AD上存在点M,使AD⊥平面PMB | B. | 异面直线AD与PB所成的角为90° | ||
| C. | 二面角P-BC-A的大小为45° | D. | BD⊥平面PAC |
分析 根据线面垂直,异面直线所成角的大小以及二面角的求解方法分别进行判断即可.
解答 解:对于A,取AD的中点M,连PM,BM,则∵侧面PAD为正三角形,
∴PM⊥AD,
又底面ABCD是∠DAB=60°的菱形,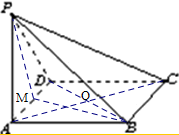
∴三角形ABD是等边三角形,
∴AD⊥BM,
∴AD⊥平面PBM,故A正确,
对于B,∵AD⊥平面PBM,
∴AD⊥PB,即异面直线AD与PB所成的角为90°,故B正确,
对于C,∵底面ABCD为菱形,∠DAB=60°平面PAD⊥平面ABCD,
∴BM⊥BC,则∠PBM是二面角P-BC-A的平面角,
设AB=1,则BM=$\frac{\sqrt{3}}{2}$,PM=$\frac{\sqrt{3}}{2}$,
在直角三角形PBM中,tan∠PBM=$\frac{PM}{BM}=1$,
即∠PBM=45°,故二面角P-BC-A的大小为45°,故C正确,
故错误的是D,
故选:D.
点评 本题主要考查空间直线和平面位置关系以及二面角的求解,根据相应的判断和证明方法是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6.x2>0是x>0的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也必要条件 |
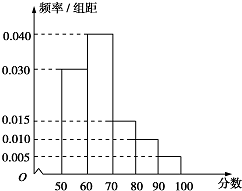 某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.
某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.