题目内容
（本小题满分12分）
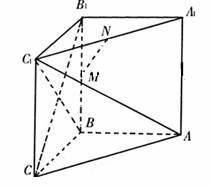如图所示，在直三棱柱ABC—A1B1C1中，∠ABC=90°，BC=CC1，M、N分别为BB1、A1C1的中点.
（Ⅰ）求证：CB1⊥平面ABC1；
（Ⅱ）求证：MN//平面ABC1.
（本小题满分12分）
解：（Ⅰ）在直三棱柱ABC—A1B1C1中，
侧面BB1C1C⊥底面ABC，且侧面BB1C1C∩底面ABC=BC，
∵∠ABC=90°，即AB⊥BC，
∴AB⊥平面BB1C1 ………………2分
∵CB1
平面BB1C1C，∴AB⊥CB1. …………… 4分
∵
，
，∴
是正方形，
∴
，∴CB1⊥平面ABC1.
（Ⅱ）取AC1的中点F，连BF、NF. ………………7分
在△AA1C1中，N、F是中点，
∴NF
AA1，又∵BM
AA1，∴EF
BM，………8分
故四边形BMNF是平行四边形，∴MN//BF，…………10分
而EF面ABC1，MN
平面ABC1，∴MN//面ABC1…12分
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
