题目内容
如右图,在直角梯形ABCD中,∠B=90°,DC∥AB,BC=CD=| 1 | 2 |
(1)若E,F分别为线段AC,AD的中点,求证:EF∥平面ABG;
(2)求证:AG⊥平面BCDG;
(3)求VC-ABD的值
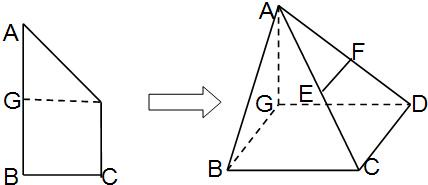
分析:(1)由题意,折叠前后CD,BG位置关系不改变得CD∥BG,由E,F分别为线段AC,AD的中点可得EF∥CD利用平行线的传递性
得EF∥BG即可得EF∥平面ABC
(2)将△ADG沿GD折起后,AG,GD位置关系不改变即得AG⊥GD,然后由平面ADG⊥平面BCDG,平面ADG∩平面BCDG=GD,
AG?面AGD 得AG⊥平面BCDG
(3)由(2)得AG⊥平面BCDG,即A到平面BCDG的距离AG=2,利用等体积法可所求几何体的体积.
得EF∥BG即可得EF∥平面ABC
(2)将△ADG沿GD折起后,AG,GD位置关系不改变即得AG⊥GD,然后由平面ADG⊥平面BCDG,平面ADG∩平面BCDG=GD,
AG?面AGD 得AG⊥平面BCDG
(3)由(2)得AG⊥平面BCDG,即A到平面BCDG的距离AG=2,利用等体积法可所求几何体的体积.
解答:(1)证明:依题意,折叠前后CD,BG位置关系不改变,∴CD∥BG
∵E,F分别为线段AC,AD的中点,∴在△ACD中,EF∥CD∴EF∥BG
∵EF?平面ABC,BG?面ABC,∴EF∥平面ABC
(2)证明:将△ADG沿GD折起后,AG,GD位置关系不改变,∴AG⊥GD
∵平面ADG⊥平面BCDG,平面ADG∩平面BCDG=GD,AG?面AGD∴AG⊥平面BCDG
(3)解:由已知得BC=CD=AG=2 又由(2)得AG⊥平面BCDG,即A到平面BCDG的距离AG=2
∴VC-ABC=VA-BCD=
S△BCD •AG=
×
×2×2×2=
.

∵E,F分别为线段AC,AD的中点,∴在△ACD中,EF∥CD∴EF∥BG
∵EF?平面ABC,BG?面ABC,∴EF∥平面ABC
(2)证明:将△ADG沿GD折起后,AG,GD位置关系不改变,∴AG⊥GD
∵平面ADG⊥平面BCDG,平面ADG∩平面BCDG=GD,AG?面AGD∴AG⊥平面BCDG
(3)解:由已知得BC=CD=AG=2 又由(2)得AG⊥平面BCDG,即A到平面BCDG的距离AG=2
∴VC-ABC=VA-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是个中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
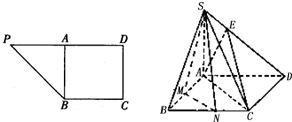

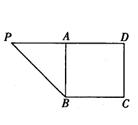
 ,BC=CD=2,PD=4,A为PD的中点,如下左图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且
,BC=CD=2,PD=4,A为PD的中点,如下左图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且 ,M,N分别是线段AB,BC的中点,如右图.
,M,N分别是线段AB,BC的中点,如右图.
 AB=2,G为线段AB的中点,将△ADG沿GD折起,使平面ADG⊥平面BCDG,得到几何体A-BCDG.
AB=2,G为线段AB的中点,将△ADG沿GD折起,使平面ADG⊥平面BCDG,得到几何体A-BCDG.