题目内容
在直角梯形PBCD中,∠D=∠C=| π |
| 2 |
| SE |
| 1 |
| 3 |
| SD |
(1)求证:SA⊥平面ABCD;
(2)求证:平面AEC∥平面SMN.
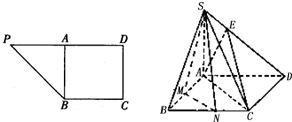
分析:(1)由已知中直角梯形PBCD中,∠D=∠C=
,BC=CD=2,PD=4,A为PD的中点,可得BA⊥PD,ABCD为正方形,进而得到SB⊥BC,AB⊥BC,故BC⊥平面SAB,由线面垂直的定义,可得BC⊥SA,又SA⊥AB,结合线面垂直的判定定理,可得SA⊥平面ABCD;
(2)连接BD,设BD∩MN=G,BD∩AC=O,连接SG,EO,利用三角形中位线定理,我们易得MN∥AC,EO∥SG,结合面面平行的判定定理,即可得到平面AEC∥平面SMN.
| π |
| 2 |
(2)连接BD,设BD∩MN=G,BD∩AC=O,连接SG,EO,利用三角形中位线定理,我们易得MN∥AC,EO∥SG,结合面面平行的判定定理,即可得到平面AEC∥平面SMN.
解答:证明:(1)由题意可知,BA⊥PD,ABCD为正方形,
所以在图中,SA⊥AB,SA=2,
四边形ABCD是边长为2的正方形,
因为SB⊥BC,AB⊥BC,
所以BC⊥平面SAB,(3分)
又SA?平面SAB,所以BC⊥SA,又SA⊥AB,
所以SA⊥平面ABCD,(6分)
(2)连接BD,设BD∩MN=G,BD∩AC=O,连接SG,EO,
正方形ABCD中,因为M,N分别是线段AB,BC的中点,所以MN∥AC,
且DO=2OG,(9分)
又SE=
SD,所以:DE=2SE,所以EO∥SG,
所以平面SMN∥平面EAC.(12分)

所以在图中,SA⊥AB,SA=2,
四边形ABCD是边长为2的正方形,
因为SB⊥BC,AB⊥BC,
所以BC⊥平面SAB,(3分)
又SA?平面SAB,所以BC⊥SA,又SA⊥AB,
所以SA⊥平面ABCD,(6分)
(2)连接BD,设BD∩MN=G,BD∩AC=O,连接SG,EO,
正方形ABCD中,因为M,N分别是线段AB,BC的中点,所以MN∥AC,
且DO=2OG,(9分)
又SE=
| 1 |
| 3 |
所以平面SMN∥平面EAC.(12分)

点评:本题考查的知识点是直线与平面垂直的判定,直线与平面平行的判定,熟练掌握空间中直线与平面垂直在判定定理及直线与平面平行判定定理,是解答本题的关键.

练习册系列答案
相关题目
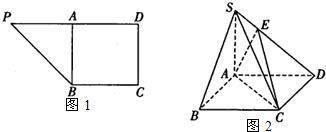 在直角梯形PBCD中,∠D=∠C=
在直角梯形PBCD中,∠D=∠C=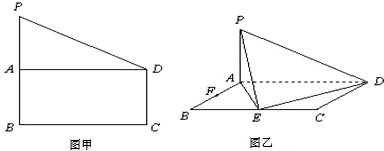
 在直角梯形PBCD中,
在直角梯形PBCD中, ,将
,将 沿AB折到
沿AB折到 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且 ,如下右图。
,如下右图。 平面ABCD;(2)求二面角E—AC—D的正切值.
平面ABCD;(2)求二面角E—AC—D的正切值.