题目内容
附加题:已知圆方程x2+y2+2y=0.(1)以圆心为焦点,顶点在原点的抛物线方程是______.
(2)求x2y2的取值范围得______.
【答案】分析:(1)先根据抛物线的顶点在坐标原点,焦点的位置,求得抛物线方程中的p,抛物线方程可得.
(2)由圆方程x2+y2+2y=0中可知x2可以用含有y的代数式来表示,利用二次函数求最值的相关知识求解.
解答:解:(1)根据顶点在坐标原点,焦点是 (-1,0)的求得
抛物线y2=2px中参数p,p=2
∴抛物线方程为 y2=-4x.
故答案为 y2=-4x.
(2)z=x2y2=y2(-y2-2y)=-y4-2y3(其中-2≤y≤0),
当y=- 时,z有最大值
时,z有最大值 ,
,
当y=-2或0时,
z=0.
故x2y2∈ .
.
点评:本题主要考查了抛物线的简单性质和抛物线的标准方程,以及二次函数求最值的相关知识,解答的关键在于考生对圆锥曲线的基础知识的把握.
(2)由圆方程x2+y2+2y=0中可知x2可以用含有y的代数式来表示,利用二次函数求最值的相关知识求解.
解答:解:(1)根据顶点在坐标原点,焦点是 (-1,0)的求得
抛物线y2=2px中参数p,p=2
∴抛物线方程为 y2=-4x.
故答案为 y2=-4x.
(2)z=x2y2=y2(-y2-2y)=-y4-2y3(其中-2≤y≤0),
当y=-
 时,z有最大值
时,z有最大值 ,
,当y=-2或0时,
z=0.
故x2y2∈
 .
.点评:本题主要考查了抛物线的简单性质和抛物线的标准方程,以及二次函数求最值的相关知识,解答的关键在于考生对圆锥曲线的基础知识的把握.

练习册系列答案
相关题目
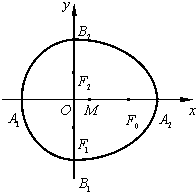 附加题:已知半椭圆
附加题:已知半椭圆 已知圆A:(x-1)2+y2=4与x轴负半轴交于B点,过B的弦BE与y轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.
已知圆A:(x-1)2+y2=4与x轴负半轴交于B点,过B的弦BE与y轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆. ,平面上点G满足
,平面上点G满足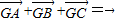 ,求点G的轨迹方程.
,求点G的轨迹方程.