题目内容
（附加题）已知圆O：x2+y2=4与x轴正半轴交于点A，在圆上另取两点B，C，使∠BAC=
，平面上点G满足
+
+
=
，求点G的轨迹方程．
| π |
| 4 |
| GA |
| GB |
| GC |
| 0 |
分析：解法1：由
+
+
=
，知点G即△ABC的重心，圆O：x2+y2=4与x轴正半轴交于点A，易知A（2，0）因为B、C在圆x2+y2=4上，故设点B（2cosθ，2sinθ）．
由重心坐标公式得轨迹的参数方程，化为普通方程即得点P的轨迹方程．
解法2：由坐标转移法同理求得点G的轨迹方程为：(x-
)2+y2=
根据
+
=2
，以 |
|=|
|，分别得到解析式，联立即可求出顶点C的轨迹E的方程．
| GA |
| GB |
| GC |
| 0 |
由重心坐标公式得轨迹的参数方程，化为普通方程即得点P的轨迹方程．
解法2：由坐标转移法同理求得点G的轨迹方程为：(x-
| 2 |
| 3 |
| 8 |
| 9 |
| GA |
| GB |
| GO |
| MC |
| MA |
解答：解：法1：由
+
+
=
，知点G即△ABC的重心，
圆O：x2+y2=4与x轴正半轴交于点A，
易知A（2，0）因为B、C在圆x2+y2=4上，故设点B（2cosθ，2sinθ）．
由∠BAC=
，则∠B0C=
，
则点C的坐标为(2cos(θ+
)，2sin(θ+
))，
由重心坐标公式得轨迹的参数方程：
（θ为参数）
即
化为普通方程是：(x-
)2+y2=
，轨迹为以点(
，0)为圆心，
为半径的圆．
法2：由∠BAC=
，则∠B0C=
，设BC的中点为P，易求得OP=
．
故点P的轨迹方程为x2+y2=2，
连接AP，因为点G为△ABC的重心，所以点G为AP的一个三等分点．
由坐标转移法同理求得点G的轨迹方程为：(x-
)2+y2=
| GA |
| GB |
| GC |
| 0 |
圆O：x2+y2=4与x轴正半轴交于点A，
易知A（2，0）因为B、C在圆x2+y2=4上，故设点B（2cosθ，2sinθ）．
由∠BAC=
| π |
| 4 |
| π |
| 2 |
则点C的坐标为(2cos(θ+
| π |
| 2 |
| π |
| 2 |
由重心坐标公式得轨迹的参数方程：
|
即
|
化为普通方程是：(x-
| 2 |
| 3 |
| 8 |
| 9 |
| 2 |
| 3 |
2
| ||
| 3 |
法2：由∠BAC=
| π |
| 4 |
| π |
| 2 |
| 2 |
故点P的轨迹方程为x2+y2=2，
连接AP，因为点G为△ABC的重心，所以点G为AP的一个三等分点．
由坐标转移法同理求得点G的轨迹方程为：(x-
| 2 |
| 3 |
| 8 |
| 9 |
点评：本题考查直线与圆锥曲线的综合问题，平面向量与共线向量，向量坐标的运算，以及求点的轨迹方程．通过运用设而不求韦达定理，方便地求出坐标的关系，考查了对知识的综合运用能力，属于中档题．
练习册系列答案
相关题目
，平面上点G满足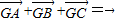
，求点G的轨迹方程．