题目内容
 已知圆A:(x-1)2+y2=4与x轴负半轴交于B点,过B的弦BE与y轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.
已知圆A:(x-1)2+y2=4与x轴负半轴交于B点,过B的弦BE与y轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.(1)求椭圆的方程;
(2)点P在椭圆C上运动,点Q在圆A上运动,求PQ+PD的最大值.
[本小问为附加题,分值5分](3)点P在椭圆C上运动,点Q在圆A上运动,求PQ+PD的最大值.
分析:(1)由B(-1,0),D(0,
),E(2,
,能求出椭圆方程.
(2)PQ+PD≤(PA+2)+PD=(PA+PD)+2PA+PD=
-PB+PD≤
+DB=2
,由此能求出PQ+PD的最大值.
| ||
| 3 |
| 3) |
(2)PQ+PD≤(PA+2)+PD=(PA+PD)+2PA+PD=
4
| ||
| 3 |
4
| ||
| 3 |
| 3 |
解答:解:(1)B(-1,0),D(0,
),E(2,
椭圆方程为
x2+3y2=1…7分
(2)PQ+PD≤(PA+2)+PD
=(PA+PD)+2PA+PD=
-PB+PD≤
+DB=2
所以P在DB延长线与椭圆交点处,
Q在PA延长线与圆的交点处,
得到最大值为2+2
. …15分
| ||
| 3 |
| 3) |
椭圆方程为
| 3 |
| 4 |
(2)PQ+PD≤(PA+2)+PD
=(PA+PD)+2PA+PD=
4
| ||
| 3 |
4
| ||
| 3 |
| 3 |
所以P在DB延长线与椭圆交点处,
Q在PA延长线与圆的交点处,
得到最大值为2+2
| 3 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 ,曲线C是以A,B为焦点且过D点的椭圆.
,曲线C是以A,B为焦点且过D点的椭圆.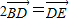 ,曲线C是以A,B为焦点且过D点的椭圆.
,曲线C是以A,B为焦点且过D点的椭圆.