题目内容
(本小题满分12分)
已知数列 ,
,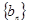 满足:
满足: ,当
,当 时,
时, ;对于任意的正整数
;对于任意的正整数 ,
,
 .设数列
.设数列 的前
的前 项和为
项和为 .
.
(Ⅰ)计算 、
、 ,并求数列
,并求数列 的通项公式;
的通项公式;
(Ⅱ)求满足 的正整数
的正整数 的集合.
的集合.
【答案】
(Ⅰ)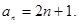 (Ⅱ)
(Ⅱ)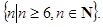
【解析】(1)由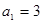 ,当
,当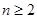 时,
时,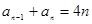 ;令
;令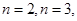 可求出
可求出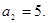
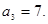 猜想
猜想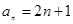 用数学归纳法证明.或者判断数列是等差数列求解;(2)由
用数学归纳法证明.或者判断数列是等差数列求解;(2)由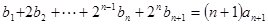 和
和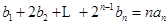
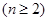 ,两式相减结合
,两式相减结合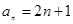 可求出
可求出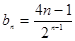 错位相减法求出
错位相减法求出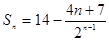 ,解不等式
,解不等式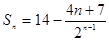
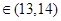 ,即
,即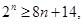 解得
解得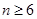 .
.
(Ⅰ)在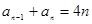 中,取
中,取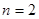 ,得
,得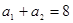 ,又
,又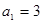 ,故
,故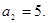
同样取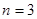 ,可得
,可得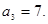
由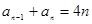 及
及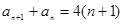 两式相减,可得
两式相减,可得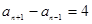 ,
,
所以数列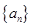 的奇数项和偶数项各自成等差数列,公差为
的奇数项和偶数项各自成等差数列,公差为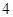 ,而
,而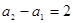 ,
,
故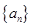 是公差为
是公差为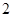 的等差数列,
的等差数列,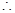
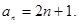 ……………………………………………… (6分)
……………………………………………… (6分)
(注:猜想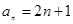 而未能证明的扣
而未能证明的扣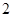 分;用数学归纳法证明不扣分.)
分;用数学归纳法证明不扣分.)
(Ⅱ)在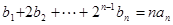 中,令
中,令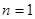 ,得
,得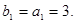
由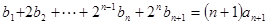 与
与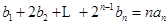
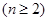 两式相减,可得
两式相减,可得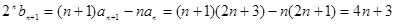 ,
,
化简,得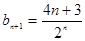 .
.
即当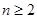 时,
时,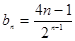 .
.
经检验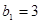 也符合该式,所以
也符合该式,所以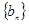 的通项公式为
的通项公式为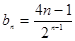 .
.
∴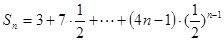 .
.
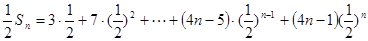 .
.
两式相减,得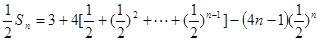 .
.
利用等比数列求和公式并化简,得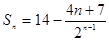 .
.
可见,对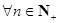 ,
,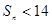 .经计算,
.经计算,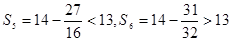 ,
,
注意到数列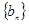 的各项为正,故
的各项为正,故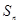 单调递增,
单调递增,
所以满足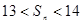 的正整数
的正整数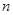 的集合为
的集合为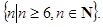 ……………………………… (12分)
……………………………… (12分)

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目