题目内容
已知 为正整数,试比较
为正整数,试比较 与
与 的大小 .
的大小 .
当n=1时, <
< ;当n=2时,
;当n=2时, =
= ; 当n=3时,
; 当n=3时, >
> ; 当n=4时,
; 当n=4时, =
= ;,当
;,当 时,
时, <
<
解析试题分析:解:当n=1时, <
< ; 1分
; 1分
当n=2时, =
= ; 2分
; 2分
当n=3时, >
> ; 3分
; 3分
当n=4时, =
= ; 4分
; 4分
当n=5时, <
< ; 当n=6时,
; 当n=6时, <
<
猜想:当 时,
时, <
< 5分
5分
下面下面用数学归纳法证明:
(1)当n=5时,由上面的探求可知猜想成立 6分
(2)假设n=k( )时猜想成立,即
)时猜想成立,即 7分
7分
则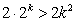 ,
,  ,
,
当 时
时
 ,从而
,从而
所以当n=k+1时,猜想也成立 9分
综合(1)(2),对 猜想都成立 10分
猜想都成立 10分
考点:数学归纳法
点评:对于不等式的证明可以通过通过对于n的讨论来得到,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 为纯虚数,
为纯虚数, 是实数,那么
是实数,那么 ( )
( )
A. | B. | C. | D. |
若复数z满足 (i是虚数单位),则z =( )
(i是虚数单位),则z =( )
A. | B.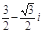 | C. | D. |
“ ”是“复数
”是“复数 (
(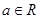 ,i为虚数单位)是纯虚数”的( )
,i为虚数单位)是纯虚数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
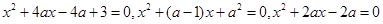 至少有一个方程有实数根.求实数
至少有一个方程有实数根.求实数 的取值范围.
的取值范围.

 在其定义域上为单调函数,求
在其定义域上为单调函数,求 的取值范围;
的取值范围; 处的切线的斜率为0,
处的切线的斜率为0, ,已知
,已知 求证:
求证:
 与
与 的大小,并说明理由.
的大小,并说明理由.  使得关于n的等式
使得关于n的等式
 …
… =
=
 都成立.
都成立.