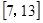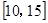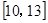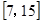题目内容
若点 和点
和点 分别为椭圆
分别为椭圆 的中心和右焦点,点
的中心和右焦点,点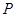 为椭圆上的任意一点,则
为椭圆上的任意一点,则 的最小值为( )
的最小值为( )
A. | B.- | C. | D.1 |
B
解析试题分析:由题意,F(1,0),设点P(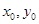 ),则有
),则有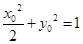 ,解得
,解得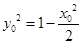 ,因为
,因为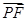 =(1?
=(1?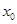 ,?
,?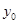 ),
),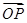 =(
=(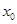 ,
,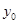 ),所以
),所以 =
=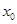 (1?
(1?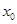 )?
)?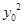 =
=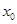 (1-
(1-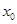 )
)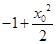 =
=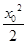 +x0?1,
+x0?1,
此二次函数对应的抛物线的对称轴为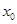 =1,因为
=1,因为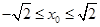 ,所以当x0=1时,则
,所以当x0=1时,则 的最大值为
的最大值为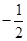 .故答案为:B.
.故答案为:B.
考点:1.椭圆的简单性质;2.平面向量数量积的运算.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
已知双曲线 的左右焦点分别是
的左右焦点分别是 ,过
,过 的直线
的直线 与双曲线相交于
与双曲线相交于 、
、 两点,则满足
两点,则满足 的直线
的直线 有 ( )
有 ( )
| A.1条 | B.2条 | C.3条 | D.4条 |
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A. | B. |
C. | D. |
若椭圆 的焦点分别为
的焦点分别为 ,弦
,弦 过点
过点 ,则
,则 的周长为
的周长为
A. | B. | C.8 | D. |
如果方程 表示双曲线,那么实数
表示双曲线,那么实数 的取值范围是( )
的取值范围是( )
A. | B. 或 或 | C. | D. 或 或 |
抛物线 的准线方程为( )
的准线方程为( )
A. | B. | C. | D. |
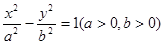 上一点
上一点 ,过双曲线中心的直线交双曲线于
,过双曲线中心的直线交双曲线于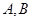 两点,记直线
两点,记直线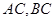 的斜率分别为
的斜率分别为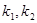 ,当
,当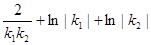 最小时,双曲线离心率为( )
最小时,双曲线离心率为( )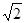 B.
B. C
C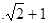 D
D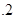
 是椭圆的两个焦点,过
是椭圆的两个焦点,过 且与椭圆长轴垂直的直线交椭圆于A、B两点,若
且与椭圆长轴垂直的直线交椭圆于A、B两点,若 是正三角形,则这个椭圆的离心率是( )
是正三角形,则这个椭圆的离心率是( ) B.
B. C.
C. D.
D.
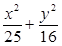 =1上一点,M、N分别是圆(x+3) 2+y2=4和(x-3) 2+y2=1上的点,则|PM|+|PN|的取值范围是 ( )
=1上一点,M、N分别是圆(x+3) 2+y2=4和(x-3) 2+y2=1上的点,则|PM|+|PN|的取值范围是 ( )