Question

已知函数f（x）=ln

x-2

x-4

+

x

4

．
（Ⅰ）求f（x）的极值；
（II）判断y=f（x）的图象是否是中心对称图形，若是求出对称中心并证明，否则说明理由；
（III）设g（x）的定义域为D，是否存在[a，b]⊆D．当x∈[a，b]时，f（x）的取值范围是[

a

4

，

b

4

]，若存在，求实数a、b的值；若不存在，说明理由．

Answer 1

分析：（I）利用导数的运算法则求出导函数，利用极值点处的导数为0，列出表格判断即可求出结果．
（II） 点（0，f（0）），（6，f（6））的中点是（3，

3

4

），所以f（x）的图象的对称中心只可能是（3，

3

4

）．方程（曲线）观点要证f（x）的图象关于（3，

3

4

）对称，只需证明点Q也在y=f（x）上，即证y₀=f（x₀）即可．
（III）假设存在实a、b且[a，b]⊆D，∴b＜2或a＞4．讨论0≤b＜2，4＜a≤6，a＜b＜0或6＜a＜b，由g（x）的单调递增区间是（-∞，0），（6，+∞），
推出f（x）的取值范围是不可能是[

a

4

，

b

4

]．因而满足条件的实数a、b不存在．

解答：20．解：（I） f′(x)=

x(x-6)

4(x-2)(x-4)

．注意到

x-2

x-4

＞ 0，即x∈（-∞，2）∪（4，+∞），
由

x(x-6)

4(x-2)(x-4)

=0得x=6或x=0．所以当x变化时，f′（x），f（x）的变化情况如下表：

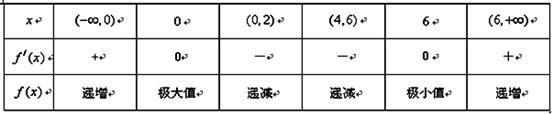
所以f（0）=ln

1

2

是f（x）的一个极大值，f（6）=ln2+

3

2

 是f（x）的一个极小值．
（II） 点（0，f（0）），（6，f（6））的中点是（3，

3

4

），所以f（x）的图象的对称中心只可能是（3，

3

4

）．
方程（曲线）观点要证f（x）的图象关于（3，

3

4

）对称，只需证明点Q也在y=f（x）上，即证y₀=f（x₀）
设P（x，y）为f（x）的图象上一点，P关于（3，

3

4

）的对称点是Q（x₀，y₀），
因

x+x0 2 =3 y+y0 2 = 3 4

?

x=6-x0 y= 3 2 -y0

，又y=ln(

x-2

x-4

)+

x

4

所以

3

2

-y0=ln(

6-x0-2

6-x0-4

)+

6-x0

4

?-y0=ln(

4-x0

2-x0

)-

x0

4

?y0=ln(

x0-2

x0-4

)+

x0

4

，
即点Q（x₀，y₀）也在函数y=f（x）的图象上．
 （III） 假设存在实a、b且[a，b]⊆D，∴b＜2或a＞4．
若0≤b＜2，当x∈[a，b]时，f（x）≤f（0）=ln

1

2

＜0，而

b

4

≥0∴f(x)≠

b

4

．故不可能…
若4＜a≤6，当x∈[a，b]时，f（x）≥f（6）=ln2+

3

2

＞

3

2

，而

a

4

≤

3

2

∴f（x）≠

a

4

．故不可能…．
若a＜b＜0或6＜a＜b，由g（x）的单调递增区间是（-∞，0），（6，+∞），知a，b是f（x）=

x

4

的两个解．而f（x）-

x

4

=ln

x-2

x-4

=0无解．故此时f的取值范f（x）围是不可能是[

a

4

，

b

4

]．
综上所述，假设错误，满足条件的实数a、b不存在．

点评：本题考查函数在极值点处的导数值为0、考查利用导数求函数的单调区间及极值，对称性问题的处理方法；注意题目中所应用的函数的思想，分类讨论的思想，函数的值域问题，利用函数的单调性验证方程解的情况．