Question

【题目】已知距离为的、两点在直线的同侧，且、到直线的距离分别为、.问能否作出经过、两点且与直线相切的圆？若能，请写出作法，画图并求出圆的半径；若不能，说明理由.

Answer 1

【答案】能够作出满足题设条件的圆

【解析】

能够作出满足题设条件的圆.

作法：1.过、两点任作一.

2.作直线交直线于.

3.过作的切线，为切点.

4.以点为圆心，为半径画弧交直线于、两点.

5.过、、三点或、、三点作或.

因此，，均为所求作的圆.

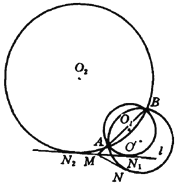
证明：是的切线，.

，.

由圆的切割线定理的逆定理知，为的切线，即与相切.

又经过、两点，因此，是符合题设条件的圆.

同理，也是符合题设条件的圆.

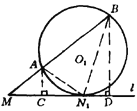
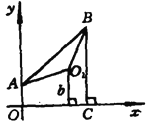
解法一：如图.过、分别作的垂线，垂足分别为、，连结、.则

.

，，，

，.

由切割线定理，得.

，.

，.

在中，由余弦定理，得.

.

.

又，

由正弦定理，得，故.

如图.连结，.，

，

.

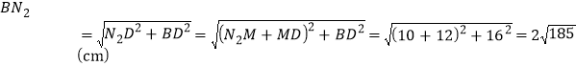在中，由余弦定理，得，.

由正弦定理，得，故.

因此，所求圆的半径为或.

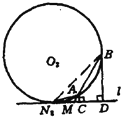
解法二：如图.以直线为轴，过点垂直于的直线为轴建立直角坐标系，于.则，有，.

设所求的圆的圆心的坐标为，则半径应为.

..

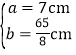解之，得或.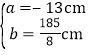

故所求圆的半径为或.

注：本题也可先求出，的值，从而由、、作圆.