题目内容
给出下列命题:
①y=1是幂函数;
②函数f(x)=2x-log2x的零点有1个;
③实数a=0.2
,b=log
0.2,c=
0.2的大小关系是b<c<a.
④设
,
,
,是单位向量,且
•
=0,则(
-
)•(
-
)的最大值为1+
⑤函数y=x+
(x≥3)的最小值为3.
其中真命题的序号是
①y=1是幂函数;
②函数f(x)=2x-log2x的零点有1个;
③实数a=0.2
| 2 |
| 2 |
| 2 |
④设
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
| 2 |
⑤函数y=x+
| 1 |
| x-1 |
其中真命题的序号是
④
④
(把你认为正确命题的序号都填上).分析:①根据幂函数的定义知,y=1是常数函数,不是幂函数;②函数f(x)=2x-log2x的零点个数即为函数y=2x与y=log2x的图象的交点个数,在同一坐标系中画出它们的图象即可;③由0<a=0.2
<1,b=log
0.2<0;④由题设条件推导出|
+
|=
.由此得到(
-
)•(
-
)=
•
-(
+
)•
+
2=1-
cos<
+
,
>,从而能判断④的正误;
⑤利用函数单调性进行判断.
| 2 |
| 2 |
| a |
| b |
| 2 |
| a |
| c |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| c |
| 2 |
| a |
| b |
| c |
⑤利用函数单调性进行判断.
解答:解:在①中,y=1是常数函数,不是幂函数.故①错误;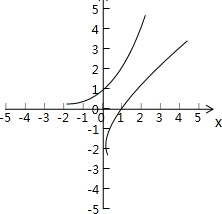
②由函数图象知:函数f(x)=2x-log2x没有零点,故②错误;
③∵0<a=0.2
<0.20=1,b=log
0.2<log
1=0,
c=
0.2>
0=1,
∴b<a<c,故③错误;
④∵
、
、
是单位向量,
•
=0,∴
⊥
,|
+
|=
.
∴(
-
)•(
-
)=
•
-(
+
)•
+
2=0-(
+
)•
+1=1-|
+
|•|
|cos<
+
,
>
=1-
cos<
+
,
>≤1+
,故④正确;
⑤∵函数y=x+
=(x-1)+
+1在[3,+∞)上是增函数,
∴当x=3时,函数y=x+
(x≥3)取最小值
,故⑤错误.
故答案为:④.
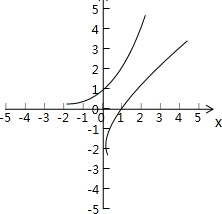
②由函数图象知:函数f(x)=2x-log2x没有零点,故②错误;
③∵0<a=0.2
| 2 |
| 2 |
| 2 |
c=
| 2 |
| 2 |
∴b<a<c,故③错误;
④∵
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| b |
| 2 |
∴(
| a |
| c |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
=1-
| 2 |
| a |
| b |
| c |
| 2 |
⑤∵函数y=x+
| 1 |
| x-1 |
| 1 |
| x-1 |
∴当x=3时,函数y=x+
| 1 |
| x-1 |
| 7 |
| 2 |
故答案为:④.
点评:此题是个基础题.考查幂函数的概念,零点的求法,平面向量问题等基础知识,考查学生灵活应用知识分析解决问题的能力.

练习册系列答案
相关题目