题目内容
（2010•汕头模拟）已知a、b、c分别是△ABC中角A、B、C的对边，且a2+c2-b2=ac．
（Ⅰ）求角B的大小； （Ⅱ）若c=3a，求tanA的值．
（Ⅰ）求角B的大小； （Ⅱ）若c=3a，求tanA的值．
分析：（Ⅰ）直接利用余弦定理即可得到结论；
（Ⅱ）先将c=3a代入a2+c2-b2=ac，得b=
a．利用余弦定理求出cosA=
=
；再根基同角三角函数之间的关系求出其正弦即可求出结论．
（Ⅱ）先将c=3a代入a2+c2-b2=ac，得b=
| 7 |
| b2+c2-a2 |
| 2bc |
5
| ||
| 14 |
解答：解：（Ⅰ）由余弦定理，得cosB=
=
（2分）
∵0＜B＜π，
∴B=
． （4分）
（Ⅱ）：将c=3a代入a2+c2-b2=ac，得b=
a． （6分）
由余弦定理，得cosA=
=
． （8分）
∵0＜A＜π，
∴sinA=
=
． （10分）
∴tanA=
=
． （12分）
| a2+c2-b2 |
| 2ac |
| 1 |
| 2 |
∵0＜B＜π，
∴B=
| π |
| 3 |
（Ⅱ）：将c=3a代入a2+c2-b2=ac，得b=
| 7 |
由余弦定理，得cosA=
| b2+c2-a2 |
| 2bc |
5
| ||
| 14 |
∵0＜A＜π，
∴sinA=
| 1-cos2A |
| ||
| 14 |
∴tanA=
| sinA |
| cosA |
| ||
| 5 |
点评：本题考查了解三角形的知识，对余弦定理及其变式进行重点考查，属于中档题目，只要细心分体已知条件式子的特点就不难解答这类问题
练习册系列答案
快乐5加2金卷系列答案
相关题目
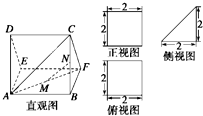（2010•汕头模拟）如图，多面体AEDBFC的直观图及三视图如图所示，M，N分别为AF，BC的中点．
（2010•汕头模拟）如图，在四边形ABCD中，设