题目内容
已知椭圆C的中心为坐标原点,焦点在y轴上,离心率e=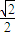 该椭圆C与直线l:y=
该椭圆C与直线l:y=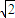 x在第一象限交于F点,且直线l被椭圆C截得的弦长为2
x在第一象限交于F点,且直线l被椭圆C截得的弦长为2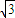 ,过F作倾斜角互补的两直线FM,FN分别与椭圆C交于M,N两点(F与M,N均不重合).
,过F作倾斜角互补的两直线FM,FN分别与椭圆C交于M,N两点(F与M,N均不重合).(I )求椭圆C的方程;
( II )求证:直线MN的斜率为定值;
(III)求三角形FMN面积的最大值.
【答案】分析:(I )由题设知:e=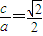 ,
,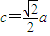 ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程.
(II)由F(1,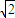 ),设kFM=k(k>0),由直线FM与FN的倾斜角互补,知kFN=-k,直线FM:
),设kFM=k(k>0),由直线FM与FN的倾斜角互补,知kFN=-k,直线FM: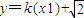 ,直线FN:
,直线FN: .由
.由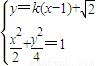 ,得
,得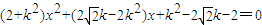 ,由
,由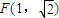 是FM与椭圆的交点,知1为(*)的一个根,另一个根为xM,
是FM与椭圆的交点,知1为(*)的一个根,另一个根为xM, ,
,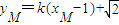 =
=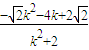 ,
,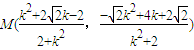 ,同理
,同理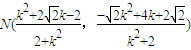 ,由此能求出直线MN的斜率为定值
,由此能求出直线MN的斜率为定值 .
.
(III)设MN与y轴交点为(0,b),M(x1,y1),N(x2,y2),又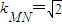 ,MN的方程为
,MN的方程为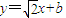 .由
.由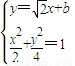 ,得
,得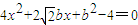 .由
.由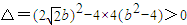 ,得b2<8,再由韦达定理和两点间距离公式进行求解.
,得b2<8,再由韦达定理和两点间距离公式进行求解.
解答:解:(I )由题设知:e=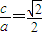 ,∴
,∴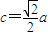 ,
,
∵c2=a2-b2,∴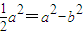 ,
,
即a2=2b2,
设所求的椭圆C的方程为 .
.
由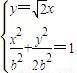 ,得
,得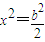 ,∴
,∴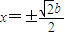 ,∴y=±b.
,∴y=±b.
∴两交点分别为(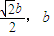 ),
),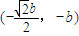 ,
,
∴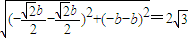 ,
,
∴b2=2,a2=4.
∴所求的椭圆C的方程为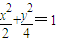 .
.
(II)由(1)知F(1,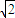 ),
),
设kFM=k(k>0),
∵直线FM与FN的倾斜角互补,
∴kFN=-k,
∴直线FM: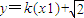 ,直线FN:
,直线FN: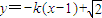 .
.
由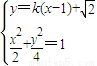 ,得
,得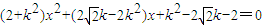 (*),
(*),
∵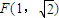 是FM与椭圆的交点,
是FM与椭圆的交点,
∴1为(*)的一个根,另一个根为xM,
∴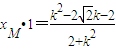 ,
,
∴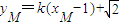
=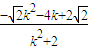 ,
,
∴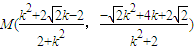 ,
,
同理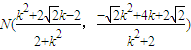 ,
,
∴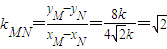 .
.
(III)设MN与y轴交点为(0,b),M(x1,y1),N(x2,y2),
又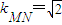 ,
,
∴MN的方程为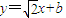 .
.
由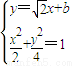 ,得
,得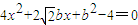 .
.
由 ,得b2<8,
,得b2<8,
∵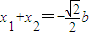 ,
,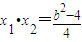 ,
,
∴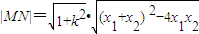
=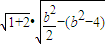
=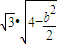 .
.
∵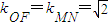 ,
,
∴OF∥MN,
∴F到MN的距离即为O到MN的距离b=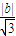 ,
,
∴
=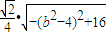 ,
,
当b2=4时,三角形FMN面积的最大值为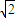 .
.
点评:本题考查椭圆方程的求法,直线斜率的计算和三角形面积的最大值的求法.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
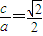 ,
,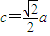 ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程.(II)由F(1,
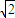 ),设kFM=k(k>0),由直线FM与FN的倾斜角互补,知kFN=-k,直线FM:
),设kFM=k(k>0),由直线FM与FN的倾斜角互补,知kFN=-k,直线FM: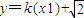 ,直线FN:
,直线FN: .由
.由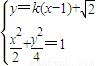 ,得
,得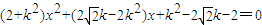 ,由
,由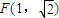 是FM与椭圆的交点,知1为(*)的一个根,另一个根为xM,
是FM与椭圆的交点,知1为(*)的一个根,另一个根为xM, ,
,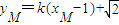 =
=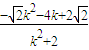 ,
,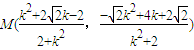 ,同理
,同理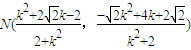 ,由此能求出直线MN的斜率为定值
,由此能求出直线MN的斜率为定值 .
.(III)设MN与y轴交点为(0,b),M(x1,y1),N(x2,y2),又
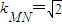 ,MN的方程为
,MN的方程为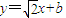 .由
.由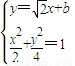 ,得
,得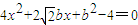 .由
.由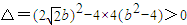 ,得b2<8,再由韦达定理和两点间距离公式进行求解.
,得b2<8,再由韦达定理和两点间距离公式进行求解.解答:解:(I )由题设知:e=
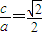 ,∴
,∴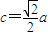 ,
,∵c2=a2-b2,∴
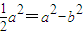 ,
,即a2=2b2,
设所求的椭圆C的方程为
 .
.由
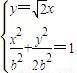 ,得
,得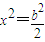 ,∴
,∴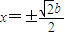 ,∴y=±b.
,∴y=±b.∴两交点分别为(
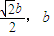 ),
),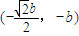 ,
,∴
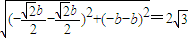 ,
,∴b2=2,a2=4.
∴所求的椭圆C的方程为
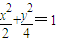 .
.(II)由(1)知F(1,
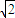 ),
),设kFM=k(k>0),
∵直线FM与FN的倾斜角互补,
∴kFN=-k,
∴直线FM:
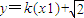 ,直线FN:
,直线FN: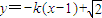 .
.由
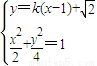 ,得
,得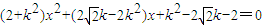 (*),
(*),∵
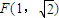 是FM与椭圆的交点,
是FM与椭圆的交点,∴1为(*)的一个根,另一个根为xM,
∴
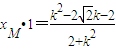 ,
,∴
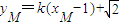
=
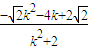 ,
,∴
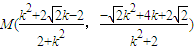 ,
,同理
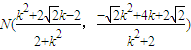 ,
,∴
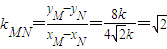 .
.(III)设MN与y轴交点为(0,b),M(x1,y1),N(x2,y2),
又
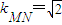 ,
,∴MN的方程为
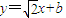 .
.由
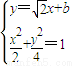 ,得
,得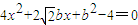 .
.由
 ,得b2<8,
,得b2<8,∵
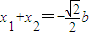 ,
,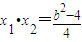 ,
,∴
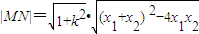
=
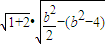
=
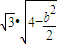 .
.∵
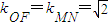 ,
,∴OF∥MN,
∴F到MN的距离即为O到MN的距离b=
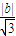 ,
,∴

=
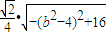 ,
,当b2=4时,三角形FMN面积的最大值为
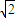 .
.点评:本题考查椭圆方程的求法,直线斜率的计算和三角形面积的最大值的求法.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目