Question

已知椭圆C的中心为坐标原点，离心率为

2

2

，直线?与椭圆C相切于M点，F₁、F₂为椭圆的左右焦点，且|MF1|+|MF2|=2

2

．
（1）求椭圆C的标准方程；
（2）若直线m过F₁点，且与椭圆相交于A、B两点，|AF2|+|BF2|=

8 2

3

，求直线m的方程．

Answer 1

分析：（1）利用椭圆的离心率，椭圆的定义，建立方程组，求出几何量，即可得到椭圆的标准方程；
（2）设出直线m的方程，与椭圆方程联立，结合韦达定理及椭圆的定义，即可求得结论．

解答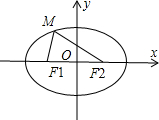：解：（1）∵椭圆的离心率为

2

2

，|MF1|+|MF2|=2

2

∴

c a = 2 2 2a=2 2

∴a=

2

，c=1
∴b=1
∴椭圆C的标准方程为

x2

2

+y2=1；
（2）由（1）知，F₁（-1，0），设直线m的方程为x=my-1
代入椭圆方程可得（m²+2）y²-2my-1=0
设A（x₁，y₁），B（x₂，y₂），则y1+y2=

2m

m2+2

，y1y2=

-1

m2+2

∴|AB|=

1+m2

|y1-y2|=

1+m2

•

( 2m m2+2 )2-4• -1 m2+2

∵|AF2|+|BF2|=

8 2

3

∴|AB|=4

2

-

8 2

3

=

4 2

3

∴

1+m2

•

( 2m m2+2 )2-4• -1 m2+2

=

4 2

3

∴m=±1
∴直线m的方程为y=±（x+1）

点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查学生的计算能力，属于中档题．