题目内容
若双曲线的离心率为2，两焦点坐标为（-2，0），（2，0），则此双曲线的方程为分析：先由题意设出焦点在x轴上的双曲线的标准方程，然后由焦点坐标易得c=2，由离心率
=2求得a，进而通过双曲线的性质b2=c2-a2求得b2，则问题解决．
| c |
| a |
解答：解：依题意设该双曲线的标准方程为
-
=1，
则c=2，e=
=2，
解得a=1，所以b2=c2-a2=4-1=3，
所以此双曲线的标准方程为x2-
=1．
故答案为x2-
=1．
| x2 |
| a2 |
| y2 |
| b2 |
则c=2，e=
| c |
| a |
解得a=1，所以b2=c2-a2=4-1=3，
所以此双曲线的标准方程为x2-
| y2 |
| 3 |
故答案为x2-
| y2 |
| 3 |
点评：本题考查双曲线的标准方程与性质．
练习册系列答案
相关题目
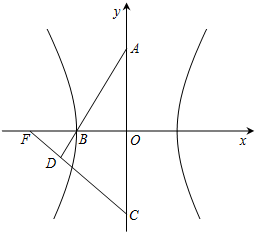如图，双曲线的中心在坐标原点O，A，C分别是双曲线虚轴的上、下顶点，B是双曲线的左顶点，F为双曲线的左焦点，直线AB与FC相交于点D．若双曲线的离心率为2，则∠BDF的余弦值是（ ）