题目内容
已知定义域为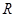 的函数
的函数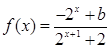 是奇函数.
是奇函数.
(Ⅰ)求实数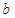 的值;
的值;
(Ⅱ)判断函数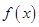 的单调性;
的单调性;
(Ⅲ)若对任意的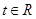 ,不等式
,不等式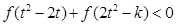 恒成立,求
恒成立,求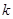 的取值范围.
的取值范围.
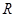 的函数
的函数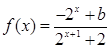 是奇函数.
是奇函数.(Ⅰ)求实数
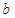 的值;
的值;(Ⅱ)判断函数
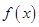 的单调性;
的单调性;(Ⅲ)若对任意的
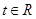 ,不等式
,不等式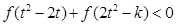 恒成立,求
恒成立,求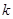 的取值范围.
的取值范围.(Ⅰ)
(Ⅱ) 在
在 上为减函数。
上为减函数。
(Ⅲ)

(Ⅱ)
 在
在 上为减函数。
上为减函数。 (Ⅲ)

试题分析:(Ⅰ)因为
 是奇函数,所以
是奇函数,所以 =0,
=0,即

(Ⅱ)由(Ⅰ)知
 ,
,设

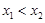 则
则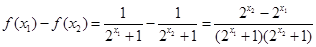
因为函数y=2
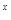 在R上是增函数且
在R上是增函数且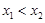 ∴
∴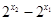 >0
>0又
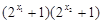 >0 ∴
>0 ∴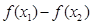 >0即
>0即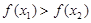
∴
 在
在 上为减函数。
上为减函数。 (Ⅲ)因
 是奇函数,从而不等式:
是奇函数,从而不等式: 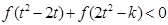
等价于
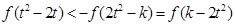 ,
,因
 为减函数,由上式推得:
为减函数,由上式推得: .即对一切
.即对一切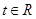 有:
有: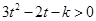 ,
,从而判别式

点评:中档题,本题将函数的奇偶性、单调性,抽象不等式的解法综合在一起考查,注重了学生综合运用数学知识处理问题能力的考查。解答过程中,注意利用转化与化归思想,将抽象不等式问题,转化成具体不等式求解,是正确解题的关键。

练习册系列答案
相关题目
 年(
年(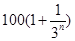 万元.设从2012年起的前
万元.设从2012年起的前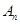 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为 万元(须扣除开发所投入资金).
万元(须扣除开发所投入资金).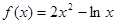 在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )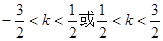
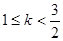
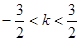
 ,曲线
,曲线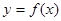 在点
在点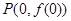 处的切线方程为
处的切线方程为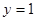
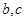 的值
的值 的三条不同切线,求
的三条不同切线,求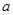 的取值范围
的取值范围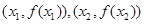 处的切线都过点(0,2),证明:当
处的切线都过点(0,2),证明:当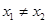 时,
时,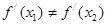
 ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围.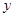 (万元)随投资收益
(万元)随投资收益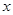 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%. 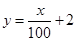 ;②
;②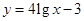 .
.
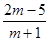 ,则实数m的取值集合是( )
,则实数m的取值集合是( )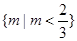
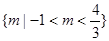
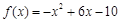 在区间[0,4]的最大值是
在区间[0,4]的最大值是 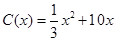 上的函数
上的函数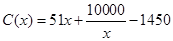 满足
满足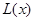 .若当
.若当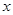 时.
时.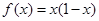 ,则当
,则当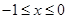 时,
时,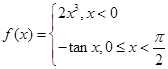 = .
= .