题目内容
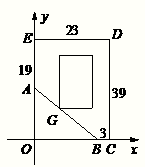
有一五边形ABCDE的地块（如图所示），其中CD，DE为围墙．其余各边界是不能动的一些体育设施．现准备在此五边形内建一栋科技楼，使楼的底面为一矩形，且靠围墙的方向须留有5米宽的空地．（Ⅰ）请设计科技楼的长和宽，使科技楼的底面面积最大？
（Ⅱ）若这一块地皮价值为400万，现用来建每层为256平方米的楼房，楼房的总建筑面积（即各层的面积之和）的每平方米平均建筑费用与建筑高度有关，楼房每升高一层，整栋楼房每平方米的建筑费用增加25元．已知建筑5层楼房时，每平方米的建筑费用为500元．为了使该楼每平方米的平均综合费用最低（综合费用是建筑费用与购地费用之和），问应把楼建成几层？
分析：（I）由图建立如图所示的坐标系，可知AB所在的直线方程，从而求出点G的坐标，最后根据矩形的面积公式求出面积，根据二次函数的性质求出最值即可；
（II）设应把楼房建成x层，则楼房的总面积为256x平方米，每平方米的购地费为4000000÷（256x）元，每平方米的建筑费用为500+500（x-5）•5%元．从而求出建房每平方米的综合费用，利用基本不等式求出最小值即可．
（II）设应把楼房建成x层，则楼房的总面积为256x平方米，每平方米的购地费为4000000÷（256x）元，每平方米的建筑费用为500+500（x-5）•5%元．从而求出建房每平方米的综合费用，利用基本不等式求出最小值即可．
解答：解：（Ⅰ）由图建立如图所示的坐标系，可知AB所在的直线方程为
+
=1，即 x+y=20，设G（x，y），由y=20-x可知G（x，20-x）．
S=（34-（20-x））（23-5-x）=-x2+4x+18•14=-（x-2）2+256．
由此可知，当x=2时，S有最大值256平方米．答：长宽均为16时面积最大．
（Ⅱ）设应把楼房建成x层，则楼房的总面积为256x平方米，每平方米的购地费为4000000÷（256x）元，每平方米的建筑费用为500+500（x-5）•5%元．
于是建房每平方米的综合费用为
y=500+500（x-5）•5%+
=375+25x+
≥375+2•
=375+1250=1625（元）．
当25x=
，即x2=
，x=
=25时，y有最小值1625．
故为了使该楼每平方米的平均综合费用最低，学校应把楼房建成25层．
| x |
| 20 |
| y |
| 20 |
S=（34-（20-x））（23-5-x）=-x2+4x+18•14=-（x-2）2+256．
由此可知，当x=2时，S有最大值256平方米．答：长宽均为16时面积最大．
（Ⅱ）设应把楼房建成x层，则楼房的总面积为256x平方米，每平方米的购地费为4000000÷（256x）元，每平方米的建筑费用为500+500（x-5）•5%元．
于是建房每平方米的综合费用为
y=500+500（x-5）•5%+
| 4000000 |
| 256x |
| 4000000 |
| 256x |
| 5•2000 |
| 16 |
当25x=
| 4000000 |
| 256x |
| 4000000 |
| 256•25 |
| 2000 |
| 16•5 |
故为了使该楼每平方米的平均综合费用最低，学校应把楼房建成25层．
点评：本题主要考查函数模型的建立和应用，主要涉及了用解析法解决平面问题，矩形面积公式，二次函数法求最值，以及数形结合的思想．
练习册系列答案
阅读快车系列答案
相关题目
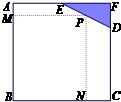（2013•杨浦区一模）如图，已知边长为8米的正方形钢板有一个角锈蚀，其中AE=4米，CD=6米．为了合理利用这块钢板，将在五边形ABCDE内截取一个矩形块BNPM，使点P在边DE上．则矩形BNPM面积的最大值为
如图所示，正五边形ABCDE的每个顶点对应着一个整数，且这五个整数的和为正数．若其3个相邻顶点对应的整数依次为x、y、z，且y＜0，则要进行如下的操作：把整数x、y、z分别换为x+y，-y，z+y，称其为一次“求正”操作．只要五个整数中有负整数，“求正”操作就要继续进行．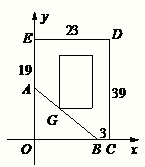
有一五边形ABCDE的地块（如图所示），其中CD，DE为围墙．其余各边界是不能动的一些体育设施．现准备在此五边形内建一栋科技楼，使楼的底面为一矩形，且靠围墙的方向须留有5米宽的空地．